Question

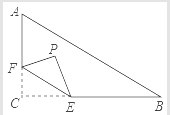
【题目】如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，若点P能落在线段AB上，则线段CF长的最小值是_____．

Answer 1

【答案】

【解析】

根据折叠的性质得到PF=CF，∠FPE=∠C=90°，PF=CE，当PF取最小值时，CF的值最小，推出当FP⊥AB时，PF的值最小，此时，点B与E重合，根据勾股定理列方程即可得到结论．

∵将△CEF沿直线EF翻折，点C落在点P处，
∴PF=CF,∠FPE=∠C=90，PF=CE，
∵当PF取最小值时，CF的值最小，
∵点P能落在线段AB上，
∴当FP⊥AB时，PF的值最小，
此时，点B与E重合，
∴BP=BC=8，
∴AP=2，AF=6CF，
∵AF2=AP2+PF2，
∴(6CF)2=22+CF2，
∴CF=，
∴CF的最小值是.