题目内容
如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.

(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.

(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
(1)通过证明 ,得AD平分∠BAC (2)半径是3
,得AD平分∠BAC (2)半径是3
 ,得AD平分∠BAC (2)半径是3
,得AD平分∠BAC (2)半径是3试题分析:(1)以AE为直径的⊙O与直角边BC相切于点D,则
 ,所以
,所以 ;直角△ABC,则
;直角△ABC,则 ,所以
,所以 ,因为AD是⊙O,⊙O与直角边BC相切于点D,所以
,因为AD是⊙O,⊙O与直角边BC相切于点D,所以 ,因此
,因此 ,所以AD平分∠BAC
,所以AD平分∠BAC(2)由图知OE、OD是圆的半径,所以OE=OD;⊙O与直角△ABC的直角边BC相切于点D,
 ,所以三角形ODB是直角三角形,由勾股定理得
,所以三角形ODB是直角三角形,由勾股定理得 ,若BE=2,BD=4,那么
,若BE=2,BD=4,那么 ,解得OD=3,所以⊙O的半径为3
,解得OD=3,所以⊙O的半径为3点评:本题考查平分线,圆的切线,勾股定理,本题考查平分线的概念和性质,圆的直径所对的圆周角为直角,圆的切线的性质,勾股定理的内容

练习册系列答案
相关题目
 分别交OA,OB于点M,N.
分别交OA,OB于点M,N.

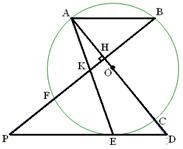
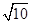 ,tan∠D=
,tan∠D=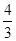 ,求DE的长.
,求DE的长. 的中点,连接PA,PB,PC.
的中点,连接PA,PB,PC. 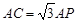 ;
;
 ,求
,求 的值.
的值.
 的距离为3,点P是直线
的距离为3,点P是直线




