题目内容
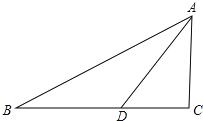
【题目】如图,大楼AB高16米,远处有一塔CD,某人在楼底B处测得塔顶的仰角为38.5°,爬到楼顶A处测得塔顶的仰角为22°,求塔高CD及大楼与塔之间的距离BD的长.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80 )
【答案】解: 过点A作AE⊥CD于点E,由题意可知:∠CAE=22°,∠CBD=38.5°,ED=AB=16米
设大楼与塔之间的距离BD的长为x米,则AE=BD=x(不设未知数x也可以)
∵在Rt△BCD中,tan∠CBD= ![]()
∴CD=BD tan 38.5°≈0.8x
∵在Rt△ACE中,tan∠CAE= ![]()
∴CE=AE tan 22°≈0.4x
∵CD﹣CE=DE
∴0.8x﹣0.4x=16
∴x=40
即BD=40(米)
CD=0.8×40=32(米)
答:塔高CD是32米,大楼与塔之间的距离BD的长为40米
【解析】过点A作AE⊥CD于点E,由题意可知:∠CAE=22°,∠CBD=38.5°,ED=AB=16米,设大楼与塔之间的距离BD的长为x米,则AE=BD=x,分别在Rt△BCD中和Rt△ACE中,用x表示出CD和CE=AE,利用CD﹣CE=DE得到有关x的方程求得x的值即可.
【考点精析】通过灵活运用关于仰角俯角问题,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.

 智慧小复习系列答案
智慧小复习系列答案【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型 | 运费 | |
运往甲地/(元/辆) | 运往乙地/(元/辆) | |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.