题目内容
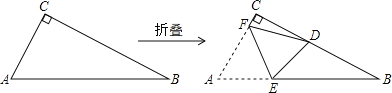
【题目】如图,![]() 网格的每个小正方形边长均为1,每个小正方形的顶点称为格点.已知
网格的每个小正方形边长均为1,每个小正方形的顶点称为格点.已知![]() 和
和![]() 的顶点都在格点上,线段
的顶点都在格点上,线段![]() 的中点为
的中点为![]() .
.
(1)以点![]() 为旋转中心,分别画出把
为旋转中心,分别画出把![]() 顺时针旋转
顺时针旋转![]() ,
,![]() 后的
后的![]() ,
,![]() ;
;
(2)利用(1)变换后所形成的图案,解答下列问题:
①直接写出四边形![]() ,四边形
,四边形![]() 的形状;
的形状;
②直接写出 的值;
的值;
③设![]() 的三边
的三边![]() ,
,![]() ,
,![]() ,请证明勾股定理.
,请证明勾股定理.

【答案】(1)见解析;(2)①正方形;②![]() ;③见解析.
;③见解析.
【解析】
(1)根据旋转作图的方法进行作图即可;
(2)①根据旋转的性质可证AC=BC1=B1C2=B2C3,从而证出四边形CC1C2C3是菱形,再根据有一个角是直角的菱形是正方形即可作出判断,同理可判断四边形ABB1B2是正方形;
②根据相似图形的面积之比等相似比的平方即可得到结果;
③用两种不同的方法计算大正方形的面积化简即可得到勾股定理.
(1)如图,
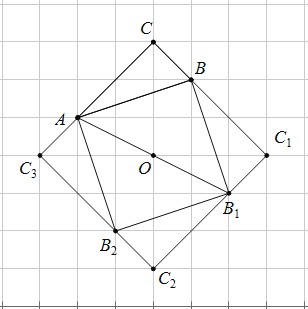
(2)①四边形CC1C2C3和四边形ABB1B2是正方形.理由如下:
∵△ABC≌△BB1C1,
∴AC=BC1,BC==B1C1,AB=BB1.
再根据旋转的性质可得:BC1=B1C2=B2C3,
B2C1=B2C2=AC3,
BB1=B1B2=AB2.
∴CC1=C1C2=C2C3=CC3
AB=BB1=B1B2=AB2
∴四边形CC1C2C3和四边形ABB1B2是菱形.
∵∠C=∠ABB1=90°,
∴四边形CC1C2C3和四边形ABB1B2是正方形.
②∵四边形CC1C2C3和四边形ABB1B2是正方形,
∴四边形CC1C2C3∽四边形ABB1B2.
∴ =
=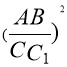
∵AB=![]() ,CC1=
,CC1=![]() ,
,
∴ =
=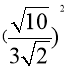 =
=![]() .
.
③ 四边形CC1C2C3的面积=![]() =
=![]() ,
,
四边形CC1C2C3的面积=4△ABC的面积+四边形ABB1B2的面积
=4![]()
![]() +
+![]() =
=![]()
∴![]() =
=![]() ,
,
化简得:![]() =
=![]() .
.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| -1 | 0 | 1 | 3 |
| -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为![]() ;③当
;③当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 有一个根大于4.其中正确的结论有( )
有一个根大于4.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个