Question

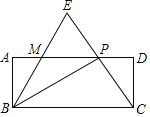
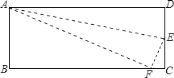
【题目】如图，在长方形中，点是上一点，连接，沿直线把折叠，使点恰好落在边上的点处.

（1）若，求的度数；

（2）若，，求线段的长度.

Answer 1

【答案】（1）；（2）20

【解析】

（1）由矩形的性质得出∠D=90°，AD∥BC，由平行线的性质得出∠DAF=∠AFB=32°，由折叠的性质得∠DAE=∠FAE=∠DAF=16°，由直角三角形的性质即可得出答案；

（2）由矩形的性质得出CD=AB=16，AD=BC，由折叠的性质得AF=AD，EF=DE=CD-CE=10，在Rt△CEF中，由勾股定理得，设BC=AD=AF=x，则BF=x-8，在Rt△ABF中，由勾股定理得出方程，解方程即可．

（1）∵四边形是长方形，

∴.

∵由翻折而得，

∴.

∴，.

∵，

∴.

由三角形内角和定理得：.

∴.

（2）∵四边形是长方形，

∴.又∵，

∴，.

∵，，

∴.

在中，由勾股定理得：.

设，则，.

在中，由勾股定理得：.解得：，

则.