��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx+c������A����3��0����B��0��3����C��1��0�����㣮
��1���������ߵĽ���ʽ�Ͷ���D�����ꣻ
��2����ͼ1���������ߵĶԳ����������ߵĶ���D˳ʱ����ת60�㣬��ֱ��y=��x���ڵ�N����ֱ��DN���Ƿ���ڵ�M��ʹ��MON=75�㣮�����ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����P��Q�ֱ���������y=ax2+bx+c��ֱ��y=��x�ϵĵ㣬���ı���OBPQ��ֱ������ʱ�������Q�����꣮
���𰸡�
��1��
�⣺�������A����3��0����B��0��3����C��1��0������y=ax2+bx+c�з�����ã�
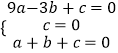 �����
����� 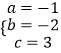 ��
��
�������ߵĽ���ʽ��y=��x2��2x+3��
��y=��x2��2x+3=����x+1��2+4��
�������ߵĶ���D������Ϊ����1��4��
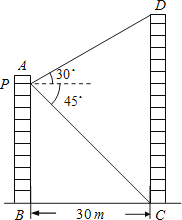
��2��
�⣺���ڣ�
���ɣ���ͼ
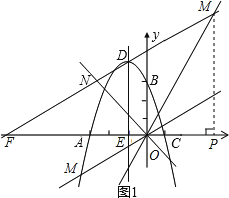
������һ����
����ת�á�EDF=60�㣬��Rt��DEF�У��ߡ�EDF=60�㣬DE=4��
��EF=DE��tan60��=4 ![]() ����OF=OE+EF=1+4
����OF=OE+EF=1+4 ![]() ��
��
��F��������� ![]() ��0����
��0����
�����D��F��ֱ�߽���ʽ��y=��x+b��
��D����1��4����F�� ![]() ��0��
��0��
������� ![]() ��
��
������������ٵ���M������ND��ʱ��
�ߡ�MON=75�㣬��BON=45�㣬
���MOB=��MON����BON=30�㣮���MOC=60�㣮
��ֱ��OM�Ľ���ʽΪy= ![]() x��
x��
���M������Ϊ�����飮 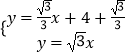 �Ľ⣬�ⷽ����ã�
�Ľ⣬�ⷽ����ã� 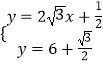 ��
��
���M�������� ![]() ��
�� ![]() ����
����
�ڵ���M������NF��ʱ�������ڵ�Mʹ�á�MON=75��
���ɣ��ߡ�MON=75�㣬��FON=45�㣬���FOM=��MON����FON=30�㣮
�ߡ�DFE=30�㣬���FOM=��DFE����OM��FN������ڣ�
�������������ڵ�M���ҵ�M������Ϊ�� ![]() ��
�� ![]() ����
����
������������M������ND�ϣ�����M��MP��x���ڵ�P��
����ת�á�EDF=60�㣬��Rt��DEF�У��ߡ�EDF=60�㣬DE=4
��EF=DE��tan60��=4 ![]() ����OF=OE��EF=1+4
����OF=OE��EF=1+4 ![]() ��
��
�ߡ�MON=75�㣬��BON=45�㣬���MOB=��MON����BON=30�㣮
���MOC=60�㣮��Rt��MOP�У���MP= ![]() OP��
OP��
��Rt��MPF����tan��MFP= ![]() ��
��
�� ![]() =
= ![]() ��
��
��OP=2 ![]() ��
�� ![]() ����MP=6��
����MP=6�� ![]() ��
��
��M��������2 ![]() ��
�� ![]() ��6��
��6�� ![]() ����
����
��M������NF�ϣ������ڵ�Mʹ�á�MON=75��
���ɣ��ߡ�MON=75�㣬��FON=45�㣬���FOM=��MON����FON=30�㣮
�ߡ�DFE=30�㣮���FOM=��DFE����OM��DN������ڣ�
�������������ڵ�M���ҵ�M������Ϊ�� ![]() ��
�� ![]() ��
��
��3��
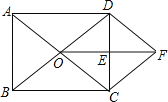
�⣺�����������ֱ������OBPQ�У�PQ��OB����OBP=90�㣮��ͼ2��

�ߡ�OBP=��AOB=90�㣬��PB��OA��
���Ե�P��B����������ͬ����3��
��Ϊ��P��������y=��x2��2x+3�ϣ�
��y=3���������ߵĽ���ʽ�е�x1=0����ȥ����x2=��2��
��PQ��OB�õ���P��Q�ĺ�������ͬ��
�����ک�2����x=��2����y=��x��y=2��
����Q�����������2��2����
����ֱ������OBPQ�У�PB��OQ����BPQ=90�㣮
��ͼ3��
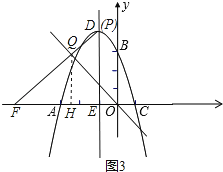
��D����1��4����B��0��3������PB��OQ����DB��OQ��
��P���������ϣ����P��D�غϣ�
���EDF=��EFD=45�㣮��EF=ED=4��
��OF=OE+EF=5��
��QH��x����H���ߡ�QOF=��QFO=45�㣬
��OQ=FQ����OH= ![]() OF=
OF= ![]() ��
��
��Q��ĺ����ꩁ ![]() ����Q����y=��x�ϣ����x=��
����Q����y=��x�ϣ����x=�� ![]() ����y=��x��y=
����y=��x��y= ![]() ����Q�����������
����Q����������� ![]() ��
�� ![]() ����
����
���ϣ����������ĵ�Q������������ֱ�Ϊ������2��2�������� ![]() ��
�� ![]() ��
��
����������1�����ô���ϵ������A��B��C����������a��b��c���ɵó�����ʽ����2���������EF�ij������ó�F������꣬�ٷ�����������ٵ���M������ND��ʱ����MON=75�㣬�ڵ���M������NF��ʱ�������ڵ�Mʹ�á�MON=75�㣬�ֱ�ó�M������꼴�ɣ���3���ֱ���ݢ�ֱ������OBPQ�У�PQ��OB����OBP=90�㣬����ֱ������OBPQ�У�PB��OQ����BPQ=90�����Q������꼴�ɣ�

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�