题目内容
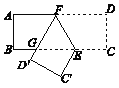
【题目】如图,点O是直线AB上的一点,OD⊥OC,过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=50°,依题意补全图形,写出求∠DOE度数的思路(不需要写出完整的推理过程);
(2)当OD绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,依题意补全图形,并求∠DOE的度数(用含α的代数式表示);
(3)当OD绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.

【答案】(1)见解析;(2)补图见解析,∠DOE=![]() α;(3)∠DOE=
α;(3)∠DOE=![]() ∠AOC或∠DOE=180°
∠AOC或∠DOE=180°![]() ∠AOC.
∠AOC.
【解析】
(1)根据角平分线的作法作出OE平分∠BOC,先根据平角的定义求出∠BOC,再根据角平分线的定义求出∠COE,再根据直角的定义即可求解;
(2)先根据平角的定义求出∠BOC,再根据角平分线的定义求出∠COE,再根据直角的定义即可求解;
(3)分两种情况:0°≤∠AOC≤180°,0°≤∠DOE≤180°,可求∠AOC与∠DOE之间的数量关系.
(1)如图1,补全图形:
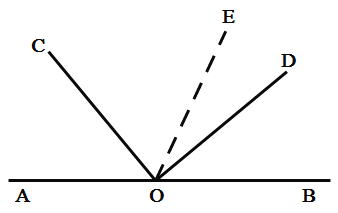
解题思路如下:
由∠AOC+∠BOC=180°,∠AOC=50°,
得∠BOC=130°;
由OE平分∠BOC,
得∠COE=65°;
由直角三角板,得∠COD=90°;
由∠COD=90°,∠COE=65°
得∠DOE=25°.
(2)如图,
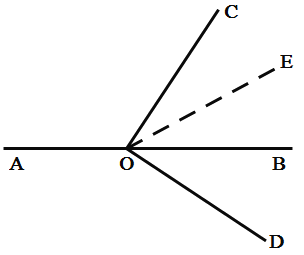
∵∠AOC+∠BOC=180°,∠AOC=α,
∴∠BOC=180°-α;
∵OE平分∠BOC,
∴∠COE=90°-![]() α;
α;
∵OD⊥OC,
∴∠COD=90°;
∴∠DOE=∠COD-∠COE=90°-(90°-![]() α)=
α)= ![]() α;
α;
(3)由(1)、(2)可得∠DOE=![]() ∠AOC(0°≤∠AOC≤180°),∠DOE=180°
∠AOC(0°≤∠AOC≤180°),∠DOE=180°![]() ∠AOC(0°≤∠DOE≤180°).
∠AOC(0°≤∠DOE≤180°).