��Ŀ����
��1����ͼ̽����
��ͼ1������A��B��ֱ��mͬ�࣬��ֱ��m������һ��P��ʹAP+BP��ֵ��С��������ͼ�ۼ�����д������
��2��ʵ�����ã�
��ͼ2���ڵȱߡ�ABC�У�AB=2����E��AB���е㣬AD�Ǹߣ���P�Ǹ�AD��һ�����㣬��BP+PE����Сֵ
��3����չ���죺
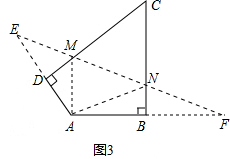
��ͼ3���ı���ABCD�У���BAD=125�㣬��B=��D=90�㣬��BC��CD�Ϸֱ���һ��M��N��ʹ��AMN�ܳ���С�������ʱ��MAN�Ķ�����

��ͼ1������A��B��ֱ��mͬ�࣬��ֱ��m������һ��P��ʹAP+BP��ֵ��С��������ͼ�ۼ�����д������
��2��ʵ�����ã�
��ͼ2���ڵȱߡ�ABC�У�AB=2����E��AB���е㣬AD�Ǹߣ���P�Ǹ�AD��һ�����㣬��BP+PE����Сֵ
��3����չ���죺
��ͼ3���ı���ABCD�У���BAD=125�㣬��B=��D=90�㣬��BC��CD�Ϸֱ���һ��M��N��ʹ��AMN�ܳ���С�������ʱ��MAN�Ķ�����

��1����ͼ1��ʾ��P�㼴Ϊ����
��2����ͼ2������EC����AD�ڵ�P��
��ʱBP+PE��С��
�ߵȱߡ�ABC�У�AB=2����E��AB���е㣬
��CE��AB��
��BE=1��BC=2��
��EC=
��
��BP+PE����СֵΪ��
��
��3����ͼ3��
�ֱ�������A����CD��BC�ĶԳƵ�E��F������EF�ֱ�CD��BC�ڵ�M��N��ʱ��AMN�ܳ���С��
�ߡ�BAD=125�㣬���E+��F=55�㣬���DAM+��EAB=��E+��F=55�㣬
���MAN=125��-55��=70�㣮
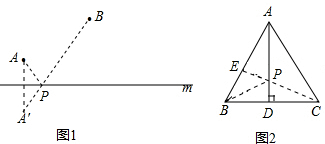
��2����ͼ2������EC����AD�ڵ�P��
��ʱBP+PE��С��
�ߵȱߡ�ABC�У�AB=2����E��AB���е㣬
��CE��AB��
��BE=1��BC=2��
��EC=
| 3 |
��BP+PE����СֵΪ��
| 3 |
��3����ͼ3��
�ֱ�������A����CD��BC�ĶԳƵ�E��F������EF�ֱ�CD��BC�ڵ�M��N��ʱ��AMN�ܳ���С��
�ߡ�BAD=125�㣬���E+��F=55�㣬���DAM+��EAB=��E+��F=55�㣬
���MAN=125��-55��=70�㣮

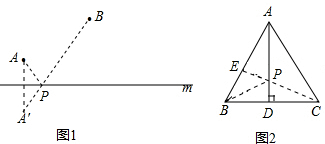

��ϰ��ϵ�д�
 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
�����Ŀ










