题目内容
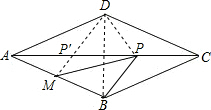
如图，菱形ABCD中，∠BAD=60°，M是AB的中点，P是对角线AC上的一个动点，若PM+PB的最小值是3，则AB长为______．
连接PD，BD，
∵PB=PD，
∴PM+PB=PM+PD，
连接MD，交AC的点就是P点，根据两点间直线最短，
∴这个P点就是要的P点，
又∵∠BAD=60°，AB=AD，
∴△ABD是等边三角形，
∵M为AB的中点，
∴MD⊥AB，
∵MD=3，
∴AD=MD÷sin60°=3÷
=2
，
∴AB=2
．
∵PB=PD，
∴PM+PB=PM+PD，
连接MD，交AC的点就是P点，根据两点间直线最短，
∴这个P点就是要的P点，
又∵∠BAD=60°，AB=AD，
∴△ABD是等边三角形，
∵M为AB的中点，
∴MD⊥AB，
∵MD=3，
∴AD=MD÷sin60°=3÷
| ||
| 2 |
| 3 |
∴AB=2
| 3 |
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
