题目内容
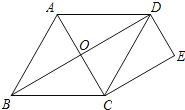
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 平分线,
平分线,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 延长线于点
延长线于点![]() .求证:
.求证:![]() .
.
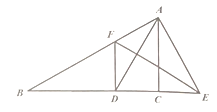
证明:∵![]() 平分
平分![]()
∴![]()
![]() (角平分线的定义)
(角平分线的定义)
∵![]() 垂直平分
垂直平分![]()
∴ ![]() (线段垂直平分线上的点到线段两个端点距离相等)
(线段垂直平分线上的点到线段两个端点距离相等)
∴![]() ( )
( )
∴![]() (等量代换)
(等量代换)
∴![]() ( )
( )
【答案】![]() ,
,![]() ;
;![]() ,
,![]() ;等边对等角;内错角相等,两直线平行.
;等边对等角;内错角相等,两直线平行.
【解析】
根据角平分线的定义,线段垂直平分线的性质,等边对等角解决问题即可.
证明:![]() AD平分∠BAC
AD平分∠BAC
∴∠BAD=∠DAC(角平分线的定义)
![]() EF垂直平分AD
EF垂直平分AD
∴FD=FA(线段垂直平分线上的点到线段两个端点距离相等)
∴∠BAD=∠ADF(等边对等角)
∴∠DAC=∠ADF(等量代换)
∴DF∥AC(内错角相等两直线平行)
故答案为:BAD,DAC,FD,FA,等边对等角,内错角相等两直线平行

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目