题目内容
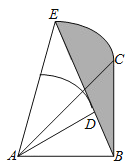
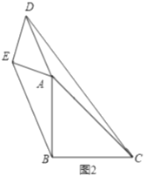
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() 的切线
的切线![]() 于点
于点![]() 交
交![]() 于点
于点![]() .
.
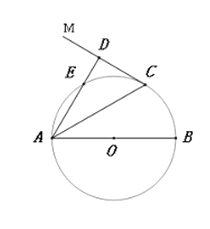
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() 求线段
求线段![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC,只要证明OC∥AD即可解决问题;
(2)连接OE,作OH⊥AD于H.只要证明△AEO是等边三角形,四边形OCDH是矩形即可解决问题.
(1)证明:连接OC,
∵CM是⊙O的切线,
∴CM⊥OC,
∵CM⊥AD,
∴OC∥AD,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠DAC=∠CAO,
∴AC平分∠BAD;
(2)连接OE,作OH⊥AD于H,
∵AE=OA=OE=2,
∴△AEO是等边三角形,
∵OH⊥AE,
∴OH=![]() ,
,
∵∠OHD=∠HDC=∠DCO=90°,
∴四边形OCDH是矩形,
∴CD=OH=![]() .
.


练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下:
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物质量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
(1)求L与x之间的函数关系;
(2)请估计重物为5kg时弹簧总长L(cm)是多少?