题目内容

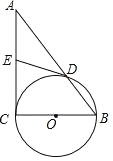
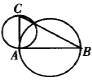
【题目】如图，Rt△ABC的斜边BC=4，∠ABC=30°，以AB、AC为直径分别作圆．则这两圆的公共部分面积为（ ）

A.B.C.D.

【答案】C

【解析】

根据割补法,将非规则图形面积转化为规则图形面积之和或差,根据扇形面积公式分别计算然后计算即可解决.

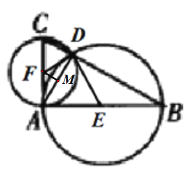
如图，E,F分别为两圆圆心，D为交点，连接AD,DE,DF

∵∠AED=30°,

∵BC=4,∠BAC=90°,

∴AC=2,AB=,

∴AF=FC=1,AE=BE=

∴∠AED=60°,

∠AFD=120°,

由题意三角形AED为等边三角形，边长为，

根据勾股定理可知其高应为，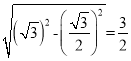

则

过点F作AD的垂线，垂足为M，

根据垂径定理可知，AM=DM,∠AFM=60°，

FM=,AM=，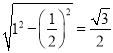

∴AD=,

则,

由题意知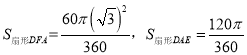

∴两圆的公共部分的面积为:

=

=

=

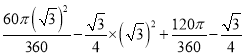
故选C.

练习册系列答案
相关题目

【题目】如图，直线y=ax+1与x轴、y轴分别相交于A、B两点，与双曲线y=（x＞0）相交于点P，PC⊥x轴于点C，且PC=2，点A的坐标为（﹣2，0）．

（1）求双曲线的解析式；

（2）若点Q为双曲线上点P右侧的一点，且QH⊥x轴于H，当以点Q、C、H为顶点的三角形与△AOB相似时，求点Q的坐标．

【题目】如图，已知直线与轴交于点，与反比例函数的图象交于，两点，的面积为.

（1）求一次函数的解析式；

（2）求点坐标和反比例函数的解析式.

【题目】如图，AB为⊙O的直径，弦CD⊥AB，垂足为点P，直线BF与AD延长线交于点F，且∠AFB＝∠ABC．

（1）求证：直线BF是⊙O的切线；

（2）若CD＝2，BP＝1，求⊙O的半径．

【题目】如图，在△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，E是AC中点．

（1）求证：DE是⊙O的切线；

（2）若AB＝10，BC＝6，连接CD，OE，交点为F，求OF的长．

【题目】如图，在平面直角坐标系中，坐标原点为O，A点坐标为(－4，0)，B点坐标为(1，0)，以AB的中点P为圆心，AB为直径作⊙P与y轴的负半轴交于点C．

（1）求经过A、B、C三点的抛物线对应的函数表达式；

（2）设M为（1）中抛物线的顶点，试说明直线MC与⊙P的位置关系，并证明你的结论；

（3）在第二象限中是否存在的一点Q，使得以A，O，Q为顶点的三角形与△OBC相似．若存在，请求出所有满足的Q点坐标；若不存在，请说明理由．

【题目】如图，抛物线与x轴交于A、B两点，与y轴交于点C，且OA=2，OC=3．

(1)求抛物线的解析式．

(2)若点D(2，2)是抛物线上一点，那么在抛物线的对称轴上，是否存在一点P，使得△BDP的周长最小，若存在，请求出点P的坐标，若不存在，请说明理由．

注：二次函数（≠0）的对称轴是直线=.

【题目】如图所示，抛物线y＝ax2+bx+c与x轴交于A、B两点，A（﹣5，0），与y轴交于C（0，﹣5），并且对称轴x＝﹣3．

（1）求抛物线的解析式；

（2）P在x轴上方的抛物线上，过P的直线y＝x+m与直线AC交于点M，与y轴交于点N，求PM+MN的最大值；

（3）点D为抛物线对称轴上一点，

①当△ACD是以AC为直角边的直角三角形时，求D点坐标；

②若△ACD是锐角三角形，求点D的纵坐标的取值范围．

【题目】如图，点在线段上，在的同侧作等腰和等腰，与、分别交于点、.对于下列结论：

①；②；③.其中正确的是（ ）

A. ①②③ B. ① C. ①② D. ②③

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网