题目内容
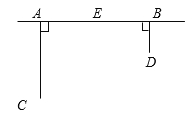
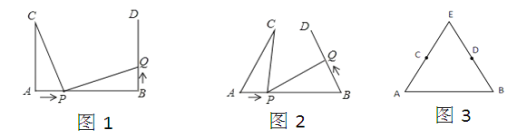
【题目】如图,AB=12cm,AC⊥AB,BD⊥AB ,AC=BD=9cm,点P在线段AB上以3 cm/s的速度,由A向B运动,同时点Q在线段BD上由B向D运动.
(1)若点Q的运动速度与点P的运动速度相等,当运动时间t=1(s),△ACP与△BPQ是否全等?说明理由,并直接判断此时线段PC和线段PQ的位置关系;
(2)将 “AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA”,其他条件不变.若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能使△ACP与△BPQ全等.
(3)在图2的基础上延长AC,BD交于点E,使C,D分别是AE,BD中点,若点Q以(2)中的运动速度从点B出发,点P以原来速度从点A同时出发,都逆时针沿△ABE三边运动,求出经过多长时间点P与点Q第一次相遇.
【答案】(1)△ACP≌△BPQ,理由见解析;线段PC与线段PQ垂直(2)1或![]() (3)9s
(3)9s
【解析】
(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;
(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
(3)因为VQ<VP,只能是点P追上点Q,即点P比点Q多走PB+BQ的路程,据此列出方程,解这个方程即可求得.
(1)当t=1时,AP=BQ=3,BP=AC=9,
又∵∠A=∠B=90°,
在△ACP与△BPQ中,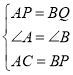 ,
,
∴△ACP≌△BPQ(SAS),
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°,
∠CPQ=90°,
则线段PC与线段PQ垂直.
(2)设点Q的运动速度x,
①若△ACP≌△BPQ,则AC=BP,AP=BQ,
![]() ,
,
解得![]() ,
,
②若△ACP≌△BPQ,则AC=BQ,AP=BP,
![]()
解得![]() ,
,
综上所述,存在![]() 或
或![]() 使得△ACP与△BPQ全等.
使得△ACP与△BPQ全等.
(3)因为VQ<VP,只能是点P追上点Q,即点P比点Q多走PB+BQ的路程,
设经过x秒后P与Q第一次相遇,
∵AC=BD=9cm,C,D分别是AE,BD的中点;
∴EB=EA=18cm.
当VQ=1时,
依题意得3x=x+2×9,
解得x=9;
当VQ=![]() 时,
时,
依题意得3x=![]() x+2×9,
x+2×9,
解得x=12.
故经过9秒或12秒时P与Q第一次相遇.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案