Question

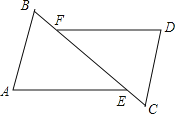
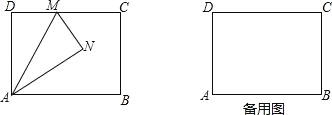
【题目】如图，在矩形 ABCD 中，AB＝4，AD＝3，M 是边 CD 上一点，将△

ADM 沿直线 AM 对折，得到△AMM．

(1)当 AN 平分∠MAB 时，求 DM 的长；

(2)连接 BN，当 DM＝1 时，求 BN 的长．

Answer 1

【答案】 (1)DM＝；(2)BN＝.

【解析】

（1）由折叠性质得∠MAN＝∠DAM，证出∠DAM＝∠MAN＝∠NAB， 由三角函数得出 DM＝ADtan∠DAM＝即可；

（2）如图，作 NE⊥AB 于 E，延长 EN 交 CD 于 F．则 NF⊥CD．利用相似三角形的性质即可解决问题.

(1)由折叠性质得：△ANM≌△ADM，

∴∠MAN＝∠DAM，

∵AN平分∠MAB，∠MAN＝∠NAB，

∴∠DAM＝∠MAN＝∠NAB，

∵四边形ABCD是矩形，

∴∠DAB＝90°，

∴∠DAM＝30°，

∴DM＝ADtan∠DAM＝3×tan30°＝3×＝；

(2)如图，作NE⊥AB于E，延长EN交CD于F，则NF⊥CD，

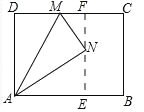
∵∠MFN＝∠MNA＝∠AEN＝90°，

∴∠MNF+∠ANE＝90°，∠ANE+∠NAE＝90°，

∴∠FNM＝∠NAE，

∴△MNF∽△NAE，

∴，

设 MF＝x，FN＝y， 则有，

解得 x＝0.8，y＝0.6，

∴AE＝1.8，NE＝2.4，BE＝AB﹣AE＝2.2

∴BN＝＝＝.