题目内容
【题目】综合与探究:
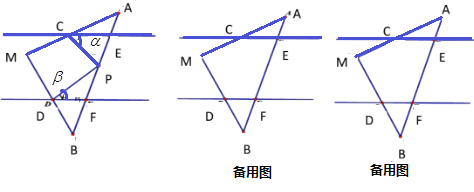
将三角形纸板如图放置,点P是边AB边上一点,DF∥CE,∠PCE=∠α,∠PDF=∠β,
探究:
(1)如果α=30°,β=40°,则∠DPC=___________.
猜想:
(2)当点P在E、F两点之间运动时,∠DPC与α、β之间有何数量关系?并说明理由;
拓展:
(3)如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),上述(2)中的结论是否还成立?并说明理由.
【答案】(1)70°;(2)∠DPC=α+β,证明详见解析;(3)∠DPC=β –α或∠DPC= α -β
【解析】
(1)过P点作GH∥DF,可得GH∥CE,根据“两直线平行,内错角相等” 解答即可;
(2)过P点作GH∥DF,可得GH∥CE,根据“两直线平行,内错角相等” 解答即可;
(3)过P点作PH∥DF,可得PH∥CE,分P点在直线CE上方、DF下方两种情况,根据“两直线平行,内错角相等” 解答即可;
(1)过P点作GH∥DF,
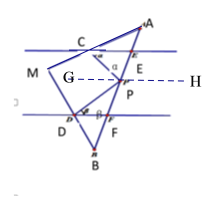
∵DF∥CE,
∴GH∥CE
∴∠PCE=∠CPG=α, ∠PDF=∠GPD=β
∵∠DPC=∠CPG+∠GPD =α+β
∵α=30°,β=40°
∴∠DPC=70°
故答案为:70°
(2)∠DPC=α+β,理由是:
如图,过P点作GH∥DF,

∵DF∥CE
∴GH∥CE
∴∠PCE=∠CPG=α, ∠PDF=∠GPD=β
∵∠DPC=∠CPG+∠GPD =α+β
(3)(2)中的结论不成立,理由是:
如图,过P作PH∥DF
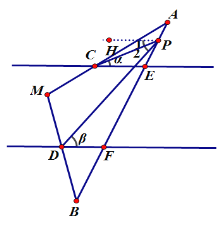
(图1)
∵DF∥CE
∴PH∥CE
∴∠PCE=∠1=α
∵∠FDP=∠2=β
∵∠DPC=∠FDP-∠PCE=∠2-∠1=β -α.
如图2,过P作PH∥DF

( 图2)
∵DF∥CE
∴PH∥CE
∴∠PCE=∠1=α
∵∠FDP=∠2=β
∵∠DPC=∠PCE-∠FDP=∠1-∠2=α -β.
故(2)中的结论不成立.

【题目】某校八年级学生某科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:
完成作业 | 单元测试 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 |
(1)若按三项成绩的平均分记为期末评价成绩,请计算小张的期末评价成绩;
(2)若按完成作业、单元检测、期末考试三项成绩按![]() 的权重来确定期末评价成绩.
的权重来确定期末评价成绩.
①请计算小张的期末评价成绩为多少分?
②小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?