题目内容
【题目】如图，在△ABC中，AC=BC=1，∠C=90°，E、F是AB上的动点，且∠ECF=45°，分别过E、F作BC、AC的垂线，垂足分别为H、G，两垂线交于点M．
（1）当点E与点B重合时，请直接写出MH与AC的数量关系 ；
（2）探索AF、EF、BE之间的数量关系，并证明你的结论；
（3）以C为坐标原点，以BC所在的直线为x轴，建立直角坐标系，请画出坐标系并利用（2）中的结论证明
．
【答案】（1）
；（2）
，证明见解析；（3）见解析．
【解析】
（1）如图1，当点
与点
重合时，点
与点重合，可得
，四边形
是矩形，进一步得到
，根据三线合一可得
，证明结论；
（2）如图2所示，将
顺时针旋转
至
，再利用
可证
，根据全等三角形的性质和勾股定理即可得出结论；
（3）由题意知四边形
是矩形，根据（2）的结论和三角形面积求法可得
，继而可知
，即可证明结论．
解： （1）结论：，
如图1，当点与点重合时，点与点重合，
，
，
，
，
，四边形是矩形，
，
，
，
，
又∵
，
；
（2）结论：，
证明：如图2所示，
，
，
．
将顺时针旋转至，
则
，
，
，
；
，
，
．
在
和
中，
，
，
．
，
，
，即；
（3）以C为坐标原点，以BC所在的直线为x轴，建立直角坐标系，如图（3）：
由（2）易知
、
、
是等腰直角三角形，
∴
，
∵
，
，
∴
，
同理可得：，
，
，
由（2）可得，
∴，
又∵
，
，
∴
．
【题目】某区对2019年参加学业水平考试的3000名初中毕业生进行了一次视力抽样调查，绘制出如下频数分布表和频数分布直方图.某区2019年初中毕业生视力抽样频数分布表
视力
| 频数/人 50 50 | 频率 0.25 0.15 |
| 60 | 0.30 |
|
| 0.25 |
| 10 |
|
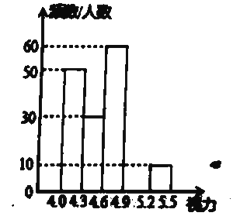
请根据图表信息回答下列问题：
（1）在频数分布表中，求
的值和
的值：
（2）将频数分布直方图补充完整；
（3）若视力在4.9以上（含4.9）均为正常，根据以上信息估计全区初中毕业生中
