ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΑΌΚœΨΤΒξΒΡ»ΐ»ΥΦδΚΆΥΪ»ΥΦδΩΆΖΩ±ξΦέΈΣΘΚ»ΐ»ΥΦδΈΣΟΩ»ΥΟΩΧλ200‘ΣΘ§ΥΪ»ΥΦδΈΣΟΩ»ΥΟΩΧλ300‘ΣΘ§ΈΣΈϋ“ΐΩΆ‘¥Θ§¥ΌΫχ¬Ο”ΈΘ§‘ΎΓΑ °“ΜΓ±ΜΤΫπ÷ήΤΎΦδΨΤΒξΫχ––”≈Μί¥σ≥ξ±ωΘ§Ζ≤Ά≈Χε»κΉΓ“Μ¬…Έε’έ”≈Μί.“ΜΗω50»ΥΒΡ¬Ο”ΈΆ≈‘Ύ °‘¬ΕΰΚ≈ΒΫΗΟΨΤΒξΉΓΥόΘ§ΉβΉΓΝΥ“Μ–©»ΐ»ΥΦδΓΔΥΪ»ΥΦδΩΆΖΩΘ°
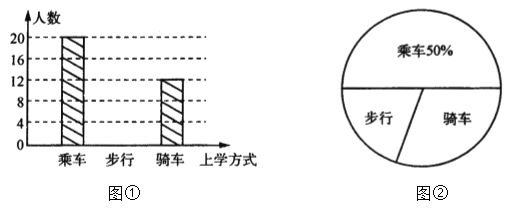
Θ®1Θ©»γΙϊΉβΉΓΒΡΟΩΗωΩΆΖΩ’ΐΚΟΉΓ¬ζΘ§≤Δ«““ΜΧλ“ΜΙ≤Μ®»ΞΉΓΥόΖ―6300‘Σ.«σΉβΉΓΝΥ»ΐ»ΥΦδΓΔΥΪ»ΥΦδΩΆΖΩΗςΕύ…ΌΦδΘΩ
Θ®2Θ©…η»ΐ»ΥΦδΙ≤ΉΓΝΥx»ΥΘ§’βΗωΆ≈“ΜΧλ“ΜΙ≤Μ®»ΞΉΓΥόΖ―y‘ΣΘ§«κ–¥≥ωy”κxΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©“ΜΧλ6300‘ΣΒΡΉΓΥόΖ― «ΖώΈΣΉνΒΆΘΩ»γΙϊ≤Μ «Θ§«κ…ηΦΤ“Μ÷÷ΖΫΑΗΘΚ“Σ«σΉβΉΓΒΡΖΩΦδ’ΐΚΟ±ΜΉΓ¬ζΒΡΘ§≤Δ ΙΉΓΥόΖ―”ΟΉνΒΆΘ§«κ–¥≥ω…ηΦΤΖΫΑΗΘ§≤Δ«σ≥ωΉνΒΆΒΡΖ―”ΟΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©8ΦδΘ§13Φδ Θ®2Θ©![]() ΓΓΘ®3Θ©≤Μ «ΘΜ»ΐ»ΥΩΆΖΩ16ΦδΘ§ΥΪ»ΥΩΆΖΩ1Φδ ±Ζ―”ΟΉνΒΆΘ§ΉνΒΆΖ―”ΟΈΣ5100‘ΣΘ°
ΓΓΘ®3Θ©≤Μ «ΘΜ»ΐ»ΥΩΆΖΩ16ΦδΘ§ΥΪ»ΥΩΆΖΩ1Φδ ±Ζ―”ΟΉνΒΆΘ§ΉνΒΆΖ―”ΟΈΣ5100‘ΣΘ°
ΓΨΫβΈωΓΩ
(1)…η»ΐ»ΥΦδ”–![]() ΦδΘ§ΥΪ»ΥΦδ”–
ΦδΘ§ΥΪ»ΥΦδ”–![]() ΦδΘ°ΉΔ“βΖ≤Ά≈Χε»κΉΓ“Μ¬…Έε’έ”≈ΜίΘ§ΗυΨίΔΌΩΆΖΩ»Υ ΐ=50ΘΜΔΎΉΓΥόΖ―6300 Ν–ΖΫ≥ΧΉι«σΫβΘΜ
ΦδΘ°ΉΔ“βΖ≤Ά≈Χε»κΉΓ“Μ¬…Έε’έ”≈ΜίΘ§ΗυΨίΔΌΩΆΖΩ»Υ ΐ=50ΘΜΔΎΉΓΥόΖ―6300 Ν–ΖΫ≥ΧΉι«σΫβΘΜ
(2)ΗυΨίΧβ“βΘ§»ΐ»ΥΦδΉΓΝΥ![]() »ΥΘ§‘ρΥΪ»ΥΦδΉΓΝΥ(
»ΥΘ§‘ρΥΪ»ΥΦδΉΓΝΥ(![]() )»ΥΘ§ΉΓΥόΖ―=100ΓΝ»ΐ»ΥΦδΒΡ»Υ ΐ+150ΓΝΥΪ»ΥΦδΒΡ»Υ ΐΘΜ
)»ΥΘ§ΉΓΥόΖ―=100ΓΝ»ΐ»ΥΦδΒΡ»Υ ΐ+150ΓΝΥΪ»ΥΦδΒΡ»Υ ΐΘΜ
(3)ΗυΨί![]() ΒΡ»Γ÷ΒΖΕΈßΦΑ ΒΦ «ιΩωΘ§‘Υ”ΟΚ· ΐΒΡ–‘÷ Ϋβ¥πΘ°
ΒΡ»Γ÷ΒΖΕΈßΦΑ ΒΦ «ιΩωΘ§‘Υ”ΟΚ· ΐΒΡ–‘÷ Ϋβ¥πΘ°
(1)…η»ΐ»ΥΦδ”–![]() ΦδΘ§ΥΪ»ΥΦδ”–
ΦδΘ§ΥΪ»ΥΦδ”–![]() ΦδΘ§
ΦδΘ§
ΗυΨίΧβ“βΒΟΘΚ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§
¥πΘΚΉβΉΓΝΥ»ΐ»ΥΦδ8ΦδΘ§ΥΪ»ΥΦδ13ΦδΘΜ
(2)ΗυΨίΧβ“βΘ§»ΐ»ΥΦδΉΓΝΥ![]() »ΥΘ§ΉΓΥόΖ―ΟΩ»Υ100‘ΣΘ§‘ρΥΪ»ΥΦδΉΓΝΥ(
»ΥΘ§ΉΓΥόΖ―ΟΩ»Υ100‘ΣΘ§‘ρΥΪ»ΥΦδΉΓΝΥ(![]() )»ΥΘ§ΉΓΥόΖ―ΟΩ»Υ150‘ΣΘ§
)»ΥΘ§ΉΓΥόΖ―ΟΩ»Υ150‘ΣΘ§
Γύ![]() ΘΜ
ΘΜ
(3)“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχΦθ–ΓΘ§
ΒΡ‘ω¥σΕχΦθ–ΓΘ§
Ι Β±![]() ¬ζΉψ
¬ζΉψ![]() ΓΔ
ΓΔ![]() ΈΣ’ϊ ΐΘ§«“
ΈΣ’ϊ ΐΘ§«“![]() Ήν¥σ ±Θ§
Ήν¥σ ±Θ§
Φ¥![]() ±Θ§ΉΓΥόΖ―”ΟΉνΒΆΘ§
±Θ§ΉΓΥόΖ―”ΟΉνΒΆΘ§
¥Υ ±![]() Θ§
Θ§
¥πΘΚ“ΜΧλ6300‘ΣΒΡΉΓΥόΖ―≤Μ «ΉνΒΆΘΜ»τ48»Υ»κΉΓ»ΐ»ΥΦδΘ§‘ρΖ―”ΟΉνΒΆΘ§ΈΣ5100‘ΣΘ°
Υυ“‘ΉΓΥόΖ―”ΟΉνΒΆΒΡ…ηΦΤΖΫΑΗΈΣΘΚ48»ΥΉΓ3»ΥΦδΘ§2»ΥΉΓ2»ΥΦδΘ°

 ΟΩ»’10Ζ÷÷”ΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
ΟΩ»’10Ζ÷÷”ΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ