题目内容
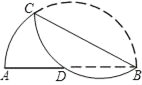
【题目】教材呈现:如图是华师版八年级上册数学教材第94页的部分内容.2.线段垂直平分线.我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴,如图,直线MN是线段AB的垂直平分线,P是MN上任一点,连结PA、PB,将线段AB沿直线MN对称,我们发现PA与PB完全重合,由此即有:线段垂直平分线的性质定理 线段垂直平分线上的点到线段的距离相等.已知:如图,MN⊥AB,垂足为点C,AC=BC,点P是直线MN上的任意一点.求证:PA=PB.图中有两个直角三角形APC和BPC,只要证明这两个三角形全等,便可证明PA=PB.

定理证明:请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.
定理应用:
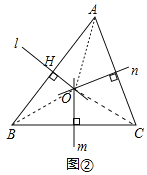
(1)如图②,在△ABC中,直线m、n分别是边BC、AC的垂直平分线,直线m、n的交点为O.过点O作OH⊥AB于点H.求证:AH=BH.
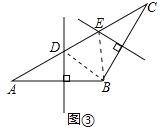
(2)如图③,在△ABC中,AB=BC,边AB的垂直平分线l交AC于点D,边BC的垂直平分线k交AC于点E.若∠ABC=120°,AC=15,则DE的长为 .
【答案】(1)见解析;(2)5
【解析】
定理证明:先证明△PAC≌△PBC,然后再运用三角形全等的性质进行解答即可;
(1)连结AO、BO、CO利用线段的垂直平分线的判定和性质即可解答;
(2)连接BD,BE,证明△BDE是等边三角形即可解答.
解:定理证明:
∵MN⊥AB,
∴∠PCA=∠PCB=90°.
又∵AC=BC,PC=PC,
∴△PAC≌△PBC(SAS),
∴PA=PB.
定理应用:(1)如图2,连结OA、OB、OC.
∵直线m是边BC的垂直平分线,
∴OB=OC,
∵直线n是边AC的垂直平分线,
∴OA=OC,
∴OA=OB
∵OH⊥AB,
∴AH=BH;
(2)如图③中,连接BD,BE.
∵BA=BC,∠ABC=120°,
∴∠A=∠C=30°,
∵边AB的垂直平分线交AC于点D,边BC的垂直平分线交AC于点E,
∴DA=DB,EB=EC,
∴∠A=∠DBA=30°,∠C=∠EBC=30°,
∴∠BDE=∠A+∠DBA=60°,∠BED=∠C+∠EBC=60°,
∴△BDE是等边三角形,
∴AD=BD=DE=BE=EC,
∵AC=15=AD+DE+EC=3DE,
∴DE=5,
故答案为:5.

【题目】工人小王生产甲、乙两种产品,生产产品件数与所用时间之间的关系如表:
生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
(1)小王每生产一件甲种产品和每生产一件乙种产品分别需要多少分钟?
(2)小王每天工作8个小时,每月工作25天.如果小王四月份生产甲种产品a件(a为正整数).
①用含a的代数式表示小王四月份生产乙种产品的件数;
②已知每生产一件甲产品可得1.50元,每生产一件乙种产品可得2.80元,若小王四月份的工资不少于1500元,求a的取值范围.