Question

【题目】如图，纸片中，，，，点在边上，以为折痕折叠得到，与边交于点，若为直角三角形，则的长是____．

Answer 1

【答案】1或

【解析】

先依据勾股定理求得AB的长，然后由翻折的性质可知：AB′＝5，DB＝DB′，接下来分为∠B′DB＝90°和∠B′ED＝90°两种情况画出图形，设DB＝DB′＝x，然后依据勾股定理列出关于x的方程求解即可．

解：∵Rt△ABC纸片中，∠C＝90°，AC＝3，BC＝4，

∴AB＝5，

∵以AD为折痕△ABD折叠得到△AB′D，

∴BD＝DB′，AB′＝AB＝10．

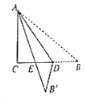
如图1所示：当∠B′DB＝90°时，过点B′作B′F⊥AF，垂足为F．

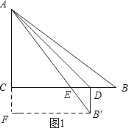
设BD＝DB′＝x，则AF＝3＋x，FB′＝4x．

在Rt△AFB′中，由勾股定理得：AB′2＝AF2＋FB′2，即（3＋x）2＋（4x）2＝52．

解得：x1＝1，x2＝0（舍去）．

∴BD＝1．

如图2所示：当∠B′ED＝90°时，C与点E重合．

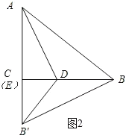
∵AB′＝5，AC＝3，

∴B′E＝2．

设BD＝DB′＝x，则DE＝4x．

在Rt△B′DE中，DB′2＝DE2＋B′E2，即x2＝（4x）2＋22．

解得：x＝．

∴BD＝．

综上所述，BD的长为1或．

故答案为1或．