题目内容
【题目】已知∠ACB=90°,AC=2,CB=4.点P为线段CB上一动点,连接AP,△APC与△APC′关于直线AP对称,其中点C的对称点为点C′.直线m过点A且平行于CB
(1)如图①:连接AB,当点C落在线段AB上时,求BC′的长;
(2)如图②:当PC=![]() BC时,延长PC′交直线m于点D,求△ADC′面积;
BC时,延长PC′交直线m于点D,求△ADC′面积;
(3)在(2)的条件下,连接BC′,直接写出线段BC′的长.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先根据勾股定理知AB=2![]() ,再由轴对称性质知AC=AC′=2,据此可得答案;
,再由轴对称性质知AC=AC′=2,据此可得答案;
(2)先轴对称性质知AC=AC′=2,PC=PC′=1,∠AC′P=90°,作C′M⊥直线m,延长MC′交BC于点N可得四边形ACNM是矩形,设C′N=x,则MC′=2﹣x,证△AMC′∽△C′NP得![]() ,据此可得AM=2x,PN=
,据此可得AM=2x,PN=![]() ,根据AM=CN=CP+PN可得x=
,根据AM=CN=CP+PN可得x=![]() ,从而得出C′N=
,从而得出C′N=![]() ,C′M=
,C′M=![]() ,AM=
,AM=![]() ,PN=
,PN=![]() ,再证△DMC′∽△PNC′得
,再证△DMC′∽△PNC′得![]() ,据此求得DM=
,据此求得DM=![]() ,最后利用三角形面积公式求解可得答案;
,最后利用三角形面积公式求解可得答案;
(3)由(2)知PB=3,PN=![]() ,C′N=
,C′N=![]() ,据此求得BN=PB﹣PN=
,据此求得BN=PB﹣PN=![]() ,利用勾股定理可得答案.
,利用勾股定理可得答案.
(1)∵AC=2,BC=4,∠ACB=90°,
∴AB=![]() ,
,
∵△APC与△APC′关于直线AP对称,
∴AC=AC′=2,
则BC′=AB﹣AC′=2![]() ﹣2;
﹣2;
(2)∵PC=![]() BC,BC=4,
BC,BC=4,
∴PC=1,BP=3,
∵△APC与△APC′关于直线AP对称,
∴AC=AC′=2,PC=PC′=1,∠AC′P=90°,
如图,过点C′作C′M⊥直线m,延长MC′交BC于点N,
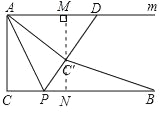
∵AD∥BC,
∴MN⊥BC,
则∠AMC′=∠C′NP=90°,
∴四边形ACNM是矩形,
∴AC=MN=2,AM=CN,
又∠AC′P=90°,
∴△AMC′∽△C′NP,
∴![]() ,
,
设C′N=x,则MC′=2﹣x,
∴![]() ,
,
解得AM=2x,PN=![]() ,
,
由AM=CN=CP+PN可得2x=1+![]() ,解得x=
,解得x=![]() ,
,
则C′N=![]() ,C′M=
,C′M=![]() ,AM=
,AM=![]() ,PN=
,PN=![]() ,
,
∵AD∥BC,
∴△DMC′∽△PNC′,
∴![]() ,即
,即![]() ,
,
解得:DM=![]() ,
,
∴AD=AM+DM=![]() ,
,
∴△ADC′面积为![]() ;
;
(3)由(2)知PB=3,PN=![]() ,C′N=
,C′N=![]() ,
,
∴BN=PB﹣PN=![]() ,
,
在Rt△BC′N中,BC′=![]() .
.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】为了鼓励市民节约用水,我市居民使用自来水计费方式实施阶梯水价,具体标准见表1,表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况.
表1:大连市居民自来水实施阶梯水价标准情况:
阶梯 | 每户年用水量(立方米) | 水价(含污水处理费)(元/立方米) |
第一阶梯 | 0~m(含m) | a |
第二阶梯 | m~240(含240) | 4.40 |
第三阶梯 | 240以上 | 7.85 |
表2:四个家庭2017年的年用水量和缴纳水费情况:
家庭 | 小明 | 小丽 | 小斌 | 小宇 |
用水量(立方米) | 50 | 100 | 200 | 220 |
水费(元) | 162.5 | 325 | 673 | 761 |
请你根据表1、表2提供的数据回答下列问题:
(1)写出表1中的a,m的值;
(2)小颖家2017年使用自来水共缴纳水费827元,则她家2017年的年用水量是多少立方米?