题目内容
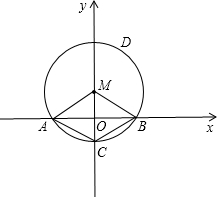 如图,已知⊙M的半径为2cm,圆心角∠AMB=120°,并建立如图所示的直角坐标系.
如图,已知⊙M的半径为2cm,圆心角∠AMB=120°,并建立如图所示的直角坐标系.
(1)求圆心M的坐标;
(2)求经过A、B、C三点抛物线的解析式;
(3)点D是位于AB所对的优弧上一动点,求四边形ACBD的最大面积;
(4)在(2)中的抛物线上是否存在一点P,使△PAB和△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)由题意知:∠AMB=120°,
∴∠CMB=60°,∠OBM=30度.
∴OM= MB=1,
MB=1,
∴M(0,1).
(2)由A,B,C三点的特殊性与对称性,知经过A,B,C三点的抛物线的解析式为y=ax2+c.
∵OC=MC-MO=1,OB=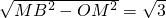 ,
,
∴C(0,-1),B( ,0).
,0).
∴c=-1,a= .
.
∴y= x2-1.
x2-1.
(3)∵S四边形ACBD=S△ABC+S△ABD,又S△ABC与AB均为定值,
∴当△ABD边AB上的高最大时,S△ABD最大,此时点D为⊙M与y轴的交点.
∴S四边形ACBD=S△ABC+S△ABD= AB•OC+
AB•OC+ AB•OD
AB•OD
= AB•CD
AB•CD
=4 cm2.
cm2.
(4)假设存在点P,如下图所示: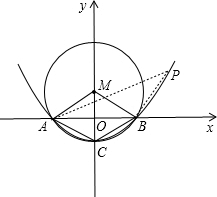
方法1:
∵△ABC为等腰三角形,∠ABC=30°,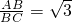 ,
,
∴△ABC∽△PAB等价于∠PAB=30°,PB=AB=2 ,PA=
,PA= PB=6.
PB=6.
设P(x,y)且x>0,则x=PA•cos30°-AO=3 -
- =2
=2  ,y=PA•sin30°=3.
,y=PA•sin30°=3.
又∵P(2 ,3)的坐标满足y=
,3)的坐标满足y= x2-1,
x2-1,
∴在抛物线y= x2-1上,存在点P(2
x2-1上,存在点P(2  ,3),
,3),
使△ABC∽△PAB.
由抛物线的对称性,知点(-2 ,3)也符合题意.
,3)也符合题意.
∴存在点P,它的坐标为(2 ,3)或(-2
,3)或(-2  ,3).
,3).
说明:只要求出(2 ,3),(-2
,3),(-2  ,3),无最后一步不扣分.下面的方法相同.
,3),无最后一步不扣分.下面的方法相同.
方法2:
当△ABC∽△PAB时,∠PAB=∠BAC=30°,又由(1)知∠MAB=30°,
∴点P在直线AM上.
设直线AM的解析式为y=kx+b,
将A(- ,0),M(0,1)代入,
,0),M(0,1)代入,
解得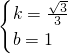 ,
,
∴直线AM的解析式为y= x+1.
x+1.
解方程组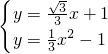 ,
,
得P(2 ,3).
,3).
又∵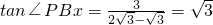 ,
,
∴∠PBx=60度.
∴∠P=30°,
∴△ABC∽△PAB.
∴在抛物线y= x2-1上,存在点(2
x2-1上,存在点(2  ,3),使△ABC∽△PAB.
,3),使△ABC∽△PAB.
由抛物线的对称性,知点(-2 ,3)也符合题意.
,3)也符合题意.
∴存在点P,它的坐标为(2 ,3)或(-2
,3)或(-2  ,3).
,3).
方法3:
∵△ABC为等腰三角形,且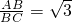 ,
,
设P(x,y),则△ABC∽△PAB等价于PB=AB=2 ,PA=
,PA= AB=6.
AB=6.
当x>0时,得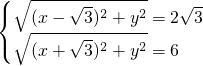 ,
,
解得P(2 ,3).
,3).
又∵P(2 ,3)的坐标满足y=
,3)的坐标满足y= x2-1,
x2-1,
∴在抛物线y= x2-1上,存在点P(2
x2-1上,存在点P(2  ,3),使△ABC∽△PAB.
,3),使△ABC∽△PAB.
由抛物线的对称性,知点(-2 ,3)也符合题意.
,3)也符合题意.
∴存在点P,它的坐标为(2 ,3)或(-2
,3)或(-2  ,3).
,3).
分析:(1)在直角△AMO中,根据三角函数就可以求出OM,就可以得到M的坐标.
(2)根据三角函数就可以求出A,B的坐标,抛物线经过点A、B、C,因而M一定是抛物线的顶点.根据待定系数法就可以求出抛物线的解析式.
(3)四边形ACBD的面积等于△ABC的面积+△ABP的面积,△ABC的面积一定,△ABP中底边AB一定,P到AB的距离最大是三角形的面积最大,即当P是圆与y轴的交点时面积最大.
(4)△PAB和△ABC相似,根据相似三角形的对应边的比相等,就可以求出P点的坐标.
点评:本题主要考查了二次函数的知识,其中涉及了待定系数法求函数的解析式、相似三角形的对应边的比相等等知识,注意熟练掌握这些知识并灵活应用.
∴∠CMB=60°,∠OBM=30度.
∴OM=
 MB=1,
MB=1,∴M(0,1).
(2)由A,B,C三点的特殊性与对称性,知经过A,B,C三点的抛物线的解析式为y=ax2+c.
∵OC=MC-MO=1,OB=
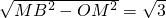 ,
,∴C(0,-1),B(
 ,0).
,0).∴c=-1,a=
 .
.∴y=
 x2-1.
x2-1.(3)∵S四边形ACBD=S△ABC+S△ABD,又S△ABC与AB均为定值,
∴当△ABD边AB上的高最大时,S△ABD最大,此时点D为⊙M与y轴的交点.
∴S四边形ACBD=S△ABC+S△ABD=
 AB•OC+
AB•OC+ AB•OD
AB•OD=
 AB•CD
AB•CD=4
 cm2.
cm2.(4)假设存在点P,如下图所示:

方法1:
∵△ABC为等腰三角形,∠ABC=30°,
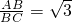 ,
,∴△ABC∽△PAB等价于∠PAB=30°,PB=AB=2
 ,PA=
,PA= PB=6.
PB=6.设P(x,y)且x>0,则x=PA•cos30°-AO=3
 -
- =2
=2  ,y=PA•sin30°=3.
,y=PA•sin30°=3.又∵P(2
 ,3)的坐标满足y=
,3)的坐标满足y= x2-1,
x2-1,∴在抛物线y=
 x2-1上,存在点P(2
x2-1上,存在点P(2  ,3),
,3),使△ABC∽△PAB.
由抛物线的对称性,知点(-2
 ,3)也符合题意.
,3)也符合题意.∴存在点P,它的坐标为(2
 ,3)或(-2
,3)或(-2  ,3).
,3).说明:只要求出(2
 ,3),(-2
,3),(-2  ,3),无最后一步不扣分.下面的方法相同.
,3),无最后一步不扣分.下面的方法相同.方法2:
当△ABC∽△PAB时,∠PAB=∠BAC=30°,又由(1)知∠MAB=30°,
∴点P在直线AM上.
设直线AM的解析式为y=kx+b,
将A(-
 ,0),M(0,1)代入,
,0),M(0,1)代入,解得
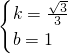 ,
,∴直线AM的解析式为y=
 x+1.
x+1.解方程组
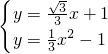 ,
,得P(2
 ,3).
,3).又∵
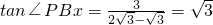 ,
,∴∠PBx=60度.
∴∠P=30°,
∴△ABC∽△PAB.
∴在抛物线y=
 x2-1上,存在点(2
x2-1上,存在点(2  ,3),使△ABC∽△PAB.
,3),使△ABC∽△PAB.由抛物线的对称性,知点(-2
 ,3)也符合题意.
,3)也符合题意.∴存在点P,它的坐标为(2
 ,3)或(-2
,3)或(-2  ,3).
,3).方法3:
∵△ABC为等腰三角形,且
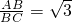 ,
,设P(x,y),则△ABC∽△PAB等价于PB=AB=2
 ,PA=
,PA= AB=6.
AB=6.当x>0时,得
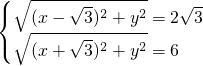 ,
,解得P(2
 ,3).
,3).又∵P(2
 ,3)的坐标满足y=
,3)的坐标满足y= x2-1,
x2-1,∴在抛物线y=
 x2-1上,存在点P(2
x2-1上,存在点P(2  ,3),使△ABC∽△PAB.
,3),使△ABC∽△PAB.由抛物线的对称性,知点(-2
 ,3)也符合题意.
,3)也符合题意.∴存在点P,它的坐标为(2
 ,3)或(-2
,3)或(-2  ,3).
,3).分析:(1)在直角△AMO中,根据三角函数就可以求出OM,就可以得到M的坐标.
(2)根据三角函数就可以求出A,B的坐标,抛物线经过点A、B、C,因而M一定是抛物线的顶点.根据待定系数法就可以求出抛物线的解析式.
(3)四边形ACBD的面积等于△ABC的面积+△ABP的面积,△ABC的面积一定,△ABP中底边AB一定,P到AB的距离最大是三角形的面积最大,即当P是圆与y轴的交点时面积最大.
(4)△PAB和△ABC相似,根据相似三角形的对应边的比相等,就可以求出P点的坐标.
点评:本题主要考查了二次函数的知识,其中涉及了待定系数法求函数的解析式、相似三角形的对应边的比相等等知识,注意熟练掌握这些知识并灵活应用.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
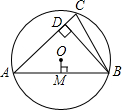 如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,弦AB=8,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A、0.6 | B、0.8 | C、0.5 | D、1.2 |
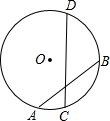 如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )
如图,已知⊙O的半径为5,两弦AB、CD相交于AB中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
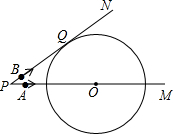 P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.
P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.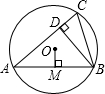 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD=
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,作BD⊥AC于点D,OM⊥AB于点M.sin∠CBD= (2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.
(2013•新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC.