题目内容
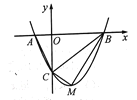
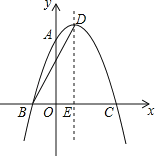
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长;
(3)点F在抛物线上运动,是否存在点F,使△BFC的面积为6,如果存在,求出点F的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)2![]() ;(3)存在,理由见解析.
;(3)存在,理由见解析.
【解析】
(1)抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),则c=3,将点B的坐标代入抛物线表达式并解得:b=2,即可求解;
(2)函数的对称轴为:x=1,则点D(1,4),则BE=2,DE=4,即可求解;
(3)△BFC的面积=![]() ×BC×|yF|=2|yF|=6,解得:yF=±3,即可求解.
×BC×|yF|=2|yF|=6,解得:yF=±3,即可求解.
解:(1)抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),
则c=3,将点B的坐标代入抛物线表达式并解得:b=2,
故抛物线的表达式为:y=﹣x2+2x+3;
(2)函数的对称轴为:x=1,则点D(1,4),
则BE=2,DE=4,
BD=![]() =2
=2![]() ;
;
(3)存在,理由:
△BFC的面积=![]() ×BC×|yF|=2|yF|=6,
×BC×|yF|=2|yF|=6,
解得:yF=±3,
故:﹣x2+2x+3=±3,
解得:x=0或2或1![]() ,
,
故点F的坐标为:(0,3)或(2,3)或(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3);
,﹣3);

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目