题目内容
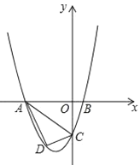
【题目】如图，抛物线
与
轴交于A，B两点，与
轴交于点C.
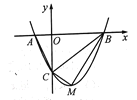
（1）请求出抛物线顶点M的坐标（用含k的代数式表示）以及A，B两点的坐标.
（2）试探究△BCM与△ABC的面积比值是否不变，若不变，试求出这个比值；若改变，请说明理由.
【答案】（1）M（1，-4k)，A（-1，0） ，B（3，0） （2）不变，
【解析】
(1)运用配方法把二次函数一般式化为顶点式,求出顶点坐标,解方程求出A、B两点的坐标;
(2)过M作MD⊥x轴于点D,根据三角形的面积公式计算即可
(1)∵
∴拋物线顶点M坐标为(1,-4k),
∵拋物线
与轴交于A.B两点,
∴当y=0时, 
=0,
∵k>0,∴x2-2x-3=0
解得：x1=﹣1，x2=3，
则A.B两点的坐标为(-1,0),(3,0);
(2)不变,
当m=0时,y=-3k,即C(0,-3k),
∴S△ABC=
过M作MD⊥x轴于点D,
则有OD=1,BD=OB-OD=2,
MD=|-4k|=4k,
S△BCM=S△BDM+S梯形OCMD－S△BOC=
+
=
=3k
S△BCM:S△ABC=3k:6k=1:2
△BCM与△ABC的面积比不变,为1:2
练习册系列答案
相关题目
【题目】某商场销售一种商品，进价为每件15元，规定每件商品售价不低于进价，且每天销售量不低于90件经调查发现，每天的销售量y（件）与每个商品的售价x（元）满足一次函数关系，其部分数据如下表所示：
每个商品的售价x（元） | … | 30 | 40 | 50 | … |
每天的销售量y（件） | … | 100 | 80 | 60 | … |
（1）填空：y与x之间的函数关系式是______.
（2）设商场每天获得的总利润为w（元），求w与x之间的函数关系式；
（3）不考虑其他因素，当商品的售价为多少元时，商场每天获得的总利润最大，最大利润是多少？
