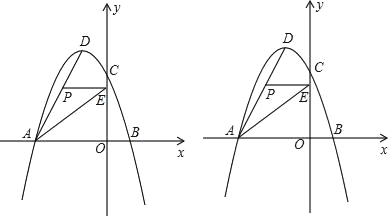题目内容
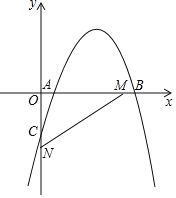
【题目】如图,平面直角坐标系中,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴的交点为C,M(3,0)与N(0,﹣2)分别是x轴、y轴上的点
(1)当m=1时,求抛物线顶点坐标.
(2)若3≤x≤3+m时,函数y=﹣x2+4x+m﹣4有最小值﹣7,求m的值.
(3)若抛物线与线段MN有公共点,直接写出m的取值范围是 .
【答案】(1)顶点坐标为(2,1);(2)m=2;(3)﹣![]() ≤m≤2.
≤m≤2.
【解析】
(1)利用配方法求顶点的坐标;
(2)根据二次函数的性质得到当x=m+3时,y有最小值﹣7,即可得到﹣(m+3)2+4(m+3)+m﹣4=﹣7,求解即可;
(3)求得直线MN的解析式,然后根据题意得到(﹣![]() )2﹣4(﹣m+2)≥0且m﹣4≤﹣2,求解即可.
)2﹣4(﹣m+2)≥0且m﹣4≤﹣2,求解即可.
解:(1)当m=1时,y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴顶点坐标为(2,1);
(2)由题意可知,该抛物线开口向下,对称轴为直线x=![]() =2,
=2,
∴当3≤x≤3+m时,y随x的增大而减小,
∴当x=m+3时,y取最小值﹣7,
∴﹣(m+3)2+4(m+3)+m﹣4=﹣7,
解得:m1=2,m2=﹣3(舍去),
∴m=2;
(3)∵M(3,0),N(0,﹣2),
设直线MN解析式为:y=kx+b(k≠0),
则![]() ,解得:
,解得: ,
,
∴直线MN的解析式为y=![]() x﹣2,
x﹣2,
∵抛物线与线段MN有公共点,则方程﹣x2+4x+m﹣4=![]() x﹣2,即x2﹣
x﹣2,即x2﹣![]() x﹣m+2=0中△≥0,且m﹣4≤﹣2,
x﹣m+2=0中△≥0,且m﹣4≤﹣2,
∴(﹣![]() )2﹣4(﹣m+2)≥0,
)2﹣4(﹣m+2)≥0,
解得:﹣![]() ≤m≤2,
≤m≤2,
故答案为:﹣![]() ≤m≤2.
≤m≤2.

 阅读快车系列答案
阅读快车系列答案【题目】某商场销售一种商品,进价为每件15元,规定每件商品售价不低于进价,且每天销售量不低于90件经调查发现,每天的销售量y(件)与每个商品的售价x(元)满足一次函数关系,其部分数据如下表所示:
每个商品的售价x(元) | … | 30 | 40 | 50 | … |
每天的销售量y(件) | … | 100 | 80 | 60 | … |
(1)填空:y与x之间的函数关系式是______.
(2)设商场每天获得的总利润为w(元),求w与x之间的函数关系式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
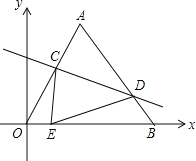
【题目】如图坐标系中,O(0,0),A(6,6![]() ),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则AC:AD的值是( )
,则AC:AD的值是( )
A.1:2B.2:3C.6:7D.7:8