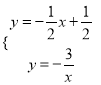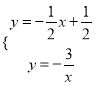ћвƒњƒЏ»Ё
°Њћвƒњ°њµ±ЌЉ–ќЊя”–ЅЏ±яѕаµ»µƒћЎ’ч ±£ђќ“√«њ…“‘∞—ЌЉ–ќµƒ“ї≤њЈ÷»∆„≈єЂє≤ґЋµг–э„™£ђ’в—щљЂЈ÷…ҐµƒћхЉюЉѓ÷–∆рјі£ђі”ґшіпµљљвЊцќ ћвµƒƒњµƒ
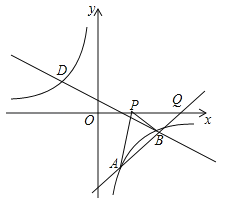
![]() »зЌЉ1£ђµ»—ь÷±љ«»эљ«–ќ
»зЌЉ1£ђµ»—ь÷±љ«»эљ«–ќ![]() ƒЏ”–“їµг
ƒЏ”–“їµг![]() Ѕђљ”
Ѕђљ”![]() ќ™ћљЊњ
ќ™ћљЊњ![]() »эћхѕяґќЉдµƒ эЅњєЎѕµ£ђќ“√«њ…“‘љЂ
»эћхѕяґќЉдµƒ эЅњєЎѕµ£ђќ“√«њ…“‘љЂ![]() »∆µг
»∆µг![]() ƒж ±’л–э„™
ƒж ±’л–э„™![]() µ√µљ
µ√µљ![]() Ѕђљ”
Ѕђљ”![]() ‘т
‘т![]() ___ ____
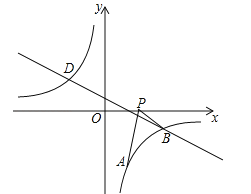
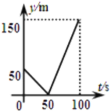
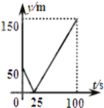
___ ____![]() «_ »эљ«–ќ£ђ
«_ »эљ«–ќ£ђ![]() »эћхѕяґќµƒ эЅњєЎѕµ «_ £ї
»эћхѕяґќµƒ эЅњєЎѕµ «_ £ї
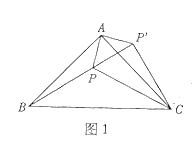
![]() »зЌЉ2£ђµ»±я»эљ«–ќ
»зЌЉ2£ђµ»±я»эљ«–ќ![]() ƒЏ“їµгP£ђЅђљ”
ƒЏ“їµгP£ђЅђљ”![]() «лљи÷ъµЏ“їќ µƒЈљЈ®ћљЊњ
«лљи÷ъµЏ“їќ µƒЈљЈ®ћљЊњ![]() »эћхѕяґќЉдµƒ эЅњєЎѕµ£Ѓ
»эћхѕяґќЉдµƒ эЅњєЎѕµ£Ѓ
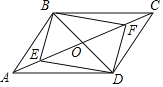
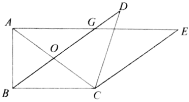
°Њір∞Є°њ£®1£© °Њљвќц°њ £®1£©ЄщЊЁ–э„™µƒ–‘÷ “„µ√ £®2£©љЂ £®3£©љЂ °а °а °яBP°Ќ °а °а Љі ‘т ‘т ‘Џ њ…÷§ ‘т![]() »зЌЉ3 £ђ‘ЏЋƒ±я–ќ
»зЌЉ3 £ђ‘ЏЋƒ±я–ќ![]() ÷–£ђ
÷–£ђ![]() µг
µг![]() ‘ЏЋƒ±я–ќƒЏ≤њ£ђ«“
‘ЏЋƒ±я–ќƒЏ≤њ£ђ«“![]()
![]() «л÷±љ”–і≥ц
«л÷±љ”–і≥ц![]() µƒ≥§£Ѓ
µƒ≥§£Ѓ
![]() £ђ÷±љ«£ђ
£ђ÷±љ«£ђ![]() £ї£®2£©
£ї£®2£©![]() £ђ÷§√чѕкЉыљвќц£ї£®3£©
£ђ÷§√чѕкЉыљвќц£ї£®3£©![]()
![]()
![]() £ђ
£ђ![]() «÷±љ«»эљ«–ќ£ђ‘ўЄщЊЁєіє…ґ®јнЉіњ…«уљв.
«÷±љ«»эљ«–ќ£ђ‘ўЄщЊЁєіє…ґ®јнЉіњ…«уљв.![]() »∆µг
»∆µг![]() Ћ≥ ±’л–э„™
Ћ≥ ±’л–э„™![]() µ√
µ√![]() Ѕђљ”
Ѕђљ”![]() њ…µ√
њ…µ√![]() ќ™µ»±я»эљ«–ќ£ђ
ќ™µ»±я»эљ«–ќ£ђ![]() £ђ‘ўЄщЊЁ
£ђ‘ўЄщЊЁ![]() јы”√єіє…ґ®јнЉіњ…«уљв.
јы”√єіє…ґ®јнЉіњ…«уљв.![]() »∆µг
»∆µг![]() Ћ≥ ±’л–э„™
Ћ≥ ±’л–э„™![]() ÷Ѕ
÷Ѕ![]() Ѕђљ”
Ѕђљ”![]() ‘т
‘т![]() £ђЄщЊЁ
£ђЄщЊЁ![]() £ђµ√µљ
£ђµ√µљ![]() £ђ‘ўЄщЊЁ
£ђ‘ўЄщЊЁ![]() £ђµ√µљ
£ђµ√µљ![]() Љі
Љі![]() £ђ‘Џ
£ђ‘Џ![]() ÷–њ…«уµ√
÷–њ…«уµ√![]() £ђ‘ўЄщЊЁ
£ђ‘ўЄщЊЁ![]() £ђњ…µ√
£ђњ…µ√![]() £ђі”ґш÷§√ч
£ђі”ґш÷§√ч![]() Љіњ…«уљв.
Љіњ…«уљв.![]() °я
°я![]() »∆µг
»∆µг![]() ƒж ±’л–э„™
ƒж ±’л–э„™![]() µ√µљ
µ√µљ![]()
![]() £ђ°ѕ
£ђ°ѕ![]() =
=![]()
![]()
![]()
![]() «÷±љ«»эљ«–ќ£Ѓ
«÷±љ«»эљ«–ќ£Ѓ![]()
![]()
![]()
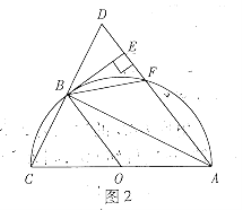
![]() »зЌЉ£ђљЂ
»зЌЉ£ђљЂ![]() »∆µг
»∆µг![]() Ћ≥ ±’л–э„™
Ћ≥ ±’л–э„™![]() µ√
µ√![]() Ѕђљ”
Ѕђљ”![]()
![]() ќ™µ»±я»эљ«–ќ£ђ
ќ™µ»±я»эљ«–ќ£ђ![]()
![]()
![]() £Ѓ
£Ѓ![]() £ЃљЂ
£ЃљЂ![]() »∆µг
»∆µг![]() Ћ≥ ±’л–э„™
Ћ≥ ±’л–э„™![]() ÷Ѕ
÷Ѕ![]() Ѕђљ”
Ѕђљ”![]()
![]() £Ѓ
£Ѓ![]()
![]() £Ѓ
£Ѓ![]() £ђ
£ђ![]() Љі
Љі![]() £Ѓ
£Ѓ![]() ÷–њ…«уµ√
÷–њ…«уµ√![]() £Ѓ
£Ѓ![]() £ђ
£ђ![]() £Ѓ
£Ѓ![]()
![]() £Ѓ
£Ѓ
ћЎ”≈∆Џƒ©Њнћ‘љрѕµЅ–ѕµЅ–ір∞Є
µ•‘™≤в ‘ABЊнЉ™Ѕ÷≥ц∞жЉѓЌ≈”–ѕё‘р»ќєЂЋЊѕµЅ–ір∞Є
–°—І”пќƒі ”п ÷≤бњ™√ч≥ц∞ж…зѕµЅ–ір∞Є
Љў∆Џ„ч“µ оЉўј÷‘∞ѕµЅ–ір∞Є
”Ґ”пћэЅ¶”л‘ƒґЅƒ№Ѕ¶—µЅЈѕµЅ–ір∞Є
–°—І±ѕ“µ…э—І„№Єіѕ∞»Ђ’жƒ£ƒв ‘ЊнѕµЅ–ір∞Є
Їм…ЂЈз±©‘§≤вЊн6ћ„ѕµЅ–ір∞Є
»Ђ≥ћњЉ∆ј∆Џƒ©“їЊнЌ®ѕµЅ–ір∞Є
–°—Іњќћ√ЅЈѕ∞ЇѕЈ є§“µіу—І≥ц∞ж…зѕµЅ–ір∞Є
Єя÷–„№Єіѕ∞µЉ”лЅЈѕµЅ–ір∞Є
°Њћвƒњ°њ÷”ƒѕ…љ‘Ї њћЄµљЈјї§–¬–ЌєЏ„і≤°ґЊЈќ—„ ±Ћµ£Ї°∞ќ“√«–и“™÷Ў ”Јјї§£ђµЂ“≤≤ї±Ўњ÷ї≈£ђЊ°Ѕњ…ў»•»Ћ‘±√№Љѓµƒ≥°Ћщ£ђ≥ц√≈ічњЏ’÷£ђ‘Џ “ƒЏ„Ґ“вЌ®Јз£ђ«Џѕі ÷£ђґа‘Ћґѓ£ђ…ў∞Њ“є£Ѓ°±ƒ≥…з«шќ™ЅЋЉ”«њ…з«шЊ”√сґ‘–¬–ЌєЏ„і≤°ґЊЈќ—„Јјї§÷™ ґµƒЅЋљв£ђЌ®єэќҐ–≈»Ї–ыіЂ–¬–ЌєЏ„і≤°ґЊЈќ—„µƒЈјї§÷™ ґ£ђ≤Ґєƒјш…з«шЊ”√с‘Џѕя≤ќ”л„чір°ґ2020ƒк–¬–ЌєЏ„і≤°ґЊЈј÷ќ»ЂєъЌ≥“їњЉ ‘£®»ЂєъЊн£©°Ј ‘Њн£®¬ъЈ÷100Ј÷£©£ђ…з«шє№јн‘±Ћжїъі””–400»Ћµƒƒ≥–°«ш≥й»°40√ы»Ћ‘±µƒірЊн≥…Љ®£ђ≤Ґґ‘Ћы√«µƒ≥…Љ®£®µ•ќї£ЇЈ÷£©Ќ≥Љ∆»зѕ¬£Ї
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
80 | 60 | 80 | 95 | 85 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
ЄщЊЁ эЊЁїж÷∆ЅЋ»зѕ¬µƒ±нЄсЇЌЌ≥Љ∆ЌЉ£Ї
µ»Љґ | ≥…Љ®£® | ∆µ¬ | ∆µ¬ |
|
| 10 | 0.25 |
|
|
| |
|
| 12 | 0.3 |
|
|
| |
ЇѕЉ∆ | 40 | 1 | |
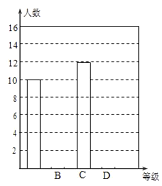
ЄщЊЁ…ѕ√жћбє©µƒ–≈ѕҐ£ђїЎірѕ¬Ѕ–ќ ћв£Ї
£®1£©Ќ≥Љ∆±н÷–µƒ![]() £ђ
£ђ![]() £ї
£ї
£®2£©«л≤є»Ђћх–ќЌ≥Љ∆ЌЉ£ї
£®3£©ЄщЊЁ≥й—щµч≤йљбєы£ђ«лєјЉ∆Є√–°«шірћв≥…Љ®ќ™°∞![]() Љґ°±µƒ”–ґа…ў»Ћ£њ
Љґ°±µƒ”–ґа…ў»Ћ£њ
£®4£©Є√…з«ш”–2√ыƒ–є№јн‘±ЇЌ2√ы≈Ѓє№јн‘±£ђѕ÷і”÷–Ћжїъћф—°2√ыє№јн‘±≤ќЉ”°∞…з«шЈјњЎ°±–ыіЂїоґѓ£ђ«л”√ ч„іЌЉЈ®їтЅ–±нЈ®«у≥ц«°Ї√—°÷–°∞1ƒ–1≈Ѓ°±µƒЄ≈¬ £Ѓ