Question

【题目】是长方形纸片的四个顶点，点分别是边上的三点，连结．

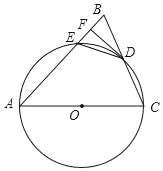
（1）将长方形纸片按图①所示的方式折叠，为折痕，点折叠后的对应点分别为，点在上，则的度数为 ；

（2）将长方形纸片按图②所示的方式折叠，为折痕，点折叠后的对应点分别为， 若， 求的度数；

（3）将长方形纸片按图③所示的方式折叠，为折痕，点折叠后的对应点分别为，若，求的度数为 ．

Answer 1

【答案】（1）90°；（2）99°；（3）180°-2m°

【解析】

（1）由折叠的性质可得，，在由角的构成可求答案；

（2）由折叠的性质可设，再根据角的构成就可求出答案；

（3）方法同（2），将（2）中的换成即可求解.

解：（1）∵沿EF，FH折叠，

∴

∵点在上，

∴，

故答案为90°；

（2）∵沿EF，FH折叠，

∴可设，

∵2x+18°+2y=180°，

∴x+y=81°

∴∠EFH=x+18°+y=99°，

故答案为99°；

（3）∵沿EF，FH折叠

∴可设

∴∠EFH=180°-∠BFE-∠CFH=180°-（x+y）

即

又∵∠

∴

故答案为：