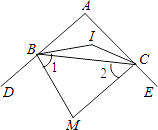
题目内容
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB, DF.
(1)求证:DF是⊙O的切线;
(2)若DB平分∠ADC,AB=a, ![]() ∶DE=4∶1,写出求DE长的思路.
∶DE=4∶1,写出求DE长的思路.
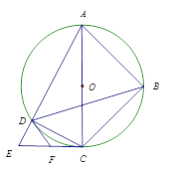
【答案】(1)证明见解析;(2)答案见解析
【解析】试题解析:(1)连接OD,由AC为圆O的直径,得∠ADC为直角,从而ΔCDE为直角,再由点F为CE的中点,得∠FDC=∠FCD,再由OD=OC得∠ODC=∠OCD,由∠FCD+∠OCD=90°得∠FDC+∠ODC=90°, 即DF是⊙O的切线;
(2)![]() 由DB平分∠ADC,AC为⊙O的直径,证明△ABC是等腰直角三角形;
由DB平分∠ADC,AC为⊙O的直径,证明△ABC是等腰直角三角形;![]() 由AB=a,求出AC的长度为
由AB=a,求出AC的长度为![]() ;
;![]() 由∠ACE=∠ADC=90°,∠CAE是公共角,证明△ACD∽△AEC,得到
由∠ACE=∠ADC=90°,∠CAE是公共角,证明△ACD∽△AEC,得到![]() ;
;![]() 设DE为x,由
设DE为x,由![]() ∶DE=4∶1,求出
∶DE=4∶1,求出![]() .
.
试题解析:(1)证明:连接OD.
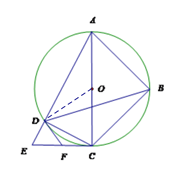
∵ OD=CD,
∴ ∠ODC=∠OCD.
∵ AC为⊙O的直径,
∴ ∠ADC=∠EDC=90°.
∵ 点F为CE的中点,
∴ DF=CF.
∴ ∠FDC=∠FCD.
∴ ∠FDO=∠FCO.
又∵ AC⊥CE,
∴ ∠FDO=∠FCO=90°.
∴ DF是⊙O的切线.
(2)①由DB平分∠ADC,AC为⊙O的直径,证明△ABC是等腰直角三角形;
②AB=a,求出AC的长度为![]() ;
;
③由∠ACE=∠ADC=90°,∠CAE是公共角,证明△ACD∽△AEC,得到![]() ;
;
④设DE为x,由![]() ∶DE=4∶1,求出
∶DE=4∶1,求出![]() .
.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】列方程或方程组解应用题:
在某场CBA比赛中,某位运动员的技术统计如下表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中 (次) | 罚球得分(分) | 篮板 (个) | 助攻(次) | 个人总得分(分) |
数据 | 38 | 27 | 11 | 6 | 3 | 4 | 33 |
注:(1)表中出手投篮次数和投中次数均不包括罚球;
(2)总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,求本场比赛中该运动员投中两分球和三分球各几个.