题目内容
【题目】如图，在△ABC中，AB=AC，∠BAC=120°，D为BC的中点，DE⊥AB于E，求EB：EA的值．
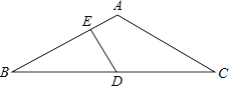
【答案】3
【解析】
连接AD，由题意易得∠B=30°，∠BAD=60°，AD⊥BC，再由DE⊥AB，可知在△ADE中，AD=2AE；在△ABD中，AB=2AD，即得AB=4AE，从而即可得出EB：EA的值．
如图，连接AD，
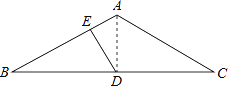
∵AB=AC，∠BAC=120°，D为BC的中点，
∴∠BAD=60°，AD⊥BC，
∴∠B=90°﹣60°=30°，
∵DE⊥AB，
∴∠ADE=90°﹣60°=30°，
设EA=x，
在Rt△ADE中，AD=2EA=2x，
在Rt△ABD中，AB=2AD=4x，
∴EB=AB﹣EA=4x﹣x=3x，
∴EB：EA=3x：x=3．
练习册系列答案
相关题目
