题目内容
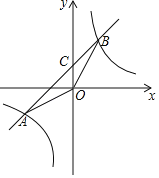
【题目】如图1,过点A(0,4)的圆的圆心坐标为C(2,0),B是第一象限圆弧上的一点,且BC⊥AC,抛物线![]() 经过C、B两点,与x轴的另一交点为D.
经过C、B两点,与x轴的另一交点为D.
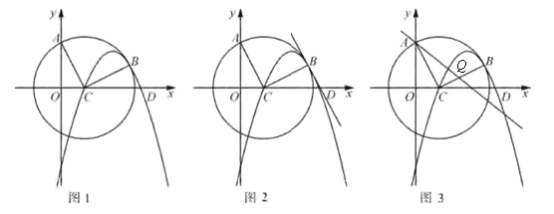
(1)点B的坐标为( , ),抛物线的表达式为 .
(2)如图2,求证:BD//AC;
(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长.
【答案】(1)(6,2)![]() (2)见解析(3)8
(2)见解析(3)8
【解析】
解:(1)过点B作BE⊥x轴于点E,
∵AC⊥BC,
∴∠ACO+∠BCE=90°,
∵∠ACO+∠OAC=90°,∠BCE+∠CBE=90°,
∴∠OAC=∠BCE,∠ACO=∠CBE.
∵在△AOC与△CEB中,

∴△AOC≌△CEB(AAS),则
CE=AO=4, BE=CO=2,OE=6,
∴B(6,2).
将B(6,2),C(2,0)代入![]() ,得
,得
![]() ,解得
,解得 .
.
∴抛物线的表达式为![]() .
.
(2)证明:令![]() ,即
,即![]() ,解得x=2或x=7.
,解得x=2或x=7.
∴D(7,0).
如下图所示,过点B作BE⊥x轴于点E,

则DE=OD-OE=1,CD=OD-OC=5.
在Rt△BDE中,由勾股定理得:![]() ;
;
在Rt△BCE中,由勾股定理得:![]()
在△BCD中,BC =![]() ,BD=
,BD=![]() ,CD=5.
,CD=5.
∴![]() .
.
∴∠CBD=90°,即BD⊥BC.
又∵ AC⊥BC,∴BD//AC.
(3)连接AB,BP,

∵AC⊥BC,BC=AC=![]() ,
,
∴∠ACB=90°,∠ABC=45°,∠APB=![]() ∠ACB=45°,AB=
∠ACB=45°,AB=![]() .
.
∴∠ABQ=∠APB.
又∵∠BAQ=∠PAB,∴△ABQ∽△APB.
∴![]() ,即
,即![]() ,解得AP=8.
,解得AP=8.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目