题目内容
【题目】如图,在正方形ABCD中,P为对角线BD上一点,MN为正方形GHMN的一边,若正方形AEOF的面积为18,则三角形PMN的面积是______.
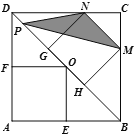
【答案】8
【解析】
根据正方形AEOF的面积为18得到正方形AEOF的边长,因为DB是对角线,能证得△DNG和△DFO是等腰直角三角形,从而得出正方形ABCD的边长,结合四边形GNMH是正方形,能得出DG=GH=HB,即可得到△PNM的面积.
解:∵正方形AEOF的面积为18,
∴AE=EO=OF=AF=![]() ,
,
∵DB是正方形的ABCD的对角线,
∴∠CDB=∠FDB =45°,
∴△DNG和△DFO是等腰直角三角形,
∴AD=![]() ,DG=GN,
,DG=GN,
同理可得:MH=HB,
∴DG=GH=HB,
∵AD=![]() ,
,
∴BD=![]() ,
,
∴GH=![]() BD=4,
BD=4,
∴△PNM的面积:MN×GN×![]() =4×4×
=4×4×![]() =8,
=8,
故答案为:8.

练习册系列答案
相关题目