��Ŀ����
����Ŀ��ij��װ���۵굽��������ѡ��A��B����Ʒ�Ƶķ�װ��������AƷ�Ʒ�װ1�ף�BƷ�Ʒ�װ1�ף�����205Ԫ��������AƷ�Ʒ�װ2�ף�BƷ�Ʒ�װ3�ף�����495Ԫ��
��1����A��B����Ʒ�Ƶķ�װÿ���۷ֱ�Ϊ����Ԫ��
��2����AƷ�Ʒ�װÿ���ۼ�Ϊ150Ԫ��BƷ�Ʒ�װÿ���ۼ�Ϊ100Ԫ�������г��������־�������BƷ�Ʒ�װ������AƷ�Ʒ�װ������2������3�ף��������BƷ�Ʒ�װ������47�ף��ҷ�װȫ���۳������ܶ����1245Ԫ���ʹ����ļ��ֽ������������ֽ�������������ࣿ����Ƕ��٣�
���𰸡���1��A��Ʒ�Ƶķ�װÿ����Ϊ120Ԫ��B��Ʒ�Ƶķ�װÿ����Ϊ85Ԫ����2�������ַ���������һ������A��Ʒ�Ʒ�װ20�ף�B��Ʒ�Ʒ�װ43�ף�������������A��Ʒ�Ʒ�װ21�ף�B��Ʒ�Ʒ�װ45�ף�������������A��Ʒ�Ʒ�װ22�ף�B��Ʒ�Ʒ�װ47�ף�����A��Ʒ�Ʒ�װ22�ף�B��Ʒ�Ʒ�װ47��ʱ��������࣬�����1365Ԫ��
��������
��1����A��Ʒ�Ƶķ�װÿ����ΪxԪ��B��Ʒ�Ƶķ�װÿ����ΪyԪ��������������AƷ�Ʒ�װ1�ף�BƷ�Ʒ�װ1�ף�����205Ԫ��������AƷ�Ʒ�װ2�ף�BƷ�Ʒ�װ3�ף�����495Ԫ�������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2���蹺��A��Ʒ�Ʒ�װm�ף���B��Ʒ�Ʒ�װ![]() �ף����ݹ���BƷ�Ʒ�װ������47���ҷ�װȫ���۳�������ܶ����1245Ԫ�����ɵó�����m��һԪһ�β���ʽ�飬��֮���ɵó�m��ȡֵ��Χ�����mΪ�������ɵó�����������������������������������ȽϺɵó����ۣ�
�ף����ݹ���BƷ�Ʒ�װ������47���ҷ�װȫ���۳�������ܶ����1245Ԫ�����ɵó�����m��һԪһ�β���ʽ�飬��֮���ɵó�m��ȡֵ��Χ�����mΪ�������ɵó�����������������������������������ȽϺɵó����ۣ�
��1����A��Ʒ�Ƶķ�װÿ����ΪxԪ��B��Ʒ�Ƶķ�װÿ����ΪyԪ
������ã�![]()
��ã�![]()
��A��Ʒ�Ƶķ�װÿ����Ϊ120Ԫ��B��Ʒ�Ƶķ�װÿ����Ϊ85Ԫ��
��2���蹺��A��Ʒ�Ʒ�װm�ף���B��Ʒ�Ʒ�װ![]() ��
��
������ã�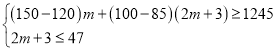
��ã�![]()
��m����
��![]()
��![]()
�������ַ���������һ������A��Ʒ�Ʒ�װ20�ף�B��Ʒ�Ʒ�װ43�ף�������������A��Ʒ�Ʒ�װ21�ף�B��Ʒ�Ʒ�װ45�ף�������������A��Ʒ�Ʒ�װ22�ף�B��Ʒ�Ʒ�װ47�ף����ַ���������ֱ����£�
![]() ��Ԫ��
��Ԫ��
![]() ��Ԫ��
��Ԫ��
![]() ��Ԫ��
��Ԫ��
��![]()
�ʹ���A��Ʒ�Ʒ�װ22�ף�B��Ʒ�Ʒ�װ47��ʱ��������࣬�����1365Ԫ��

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�