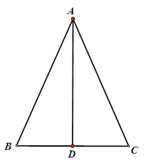
题目内容
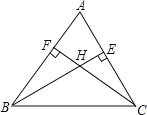
【题目】如图①,在△ABC中,CD、CE分别是△ABC的高和角平分线,∠BAC=α,∠B=β(α>β).
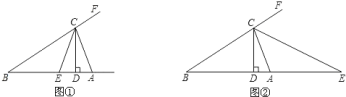
(1)若α=70°,β=40°,求∠DCE的度数;
(2)试用α、β的代数式表示∠DCE的度数(直接写出结果);
(3)如图②,若CE是△ABC外角∠ACF的平分线,交BA延长线于点E,且α﹣β=30°,求∠DCE的度数.
【答案】(1)15°;(2)![]() ;(3)75°.
;(3)75°.
【解析】
(1)三角形的内角和是180°,已知∠BAC与∠ABC的度数,则可求出∠BAC的度数,然后根据角平分线的性质求出∠BCE,再利用三角形的一个外角等于和它不相邻的两个内角的和求出∠DEC的度数,进而求出∠DCE的度数;
(2)∠DCE=![]() .
.
(3)作∠ACB的内角平分线CE′,根据角平分线的性质求出∠ECE′=∠ACE+∠ACE′=![]() ∠ACB+
∠ACB+![]() ∠ACF=90°,进而求出∠DCE的度数.
∠ACF=90°,进而求出∠DCE的度数.
解:(1)因为∠ACB=180°﹣(∠BAC+∠B)=180°﹣(70°+40°)=70°,
又因为CE是∠ACB的平分线,
所以![]() .
.
因为CD是高线,
所以∠ADC=90°,
所以∠ACD=90°﹣∠BAC=20°,
所以∠DCE=∠ACE﹣∠ACD=35°﹣20°=15°.
(2)![]() .
.
(3)如图,作∠ACB的内角平分线CE′,
则![]() .
.
因为CE是∠ACB的外角平分线,
所以∠ECE′=∠ACE+∠ACE′=![]() =
=![]() =90°,
=90°,
所以∠DCE=90°﹣∠DCE′=90°﹣15°=75°.
即∠DCE的度数为75°.

 阅读快车系列答案
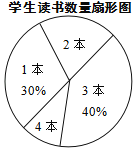
阅读快车系列答案【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?