��Ŀ����
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P��ͼ��G���������¶��壺����P�����һ����ϵķ���ƽ��һ�Σ�ƽ�ƾ���Ϊd��d��0�������ȵ�λ��ƽ�ƺ�ĵ��ΪP��������P����ͼ��G�ϣ���Ƶ�PΪͼ��G������ɵ������ر�أ�����P��ͼ��G��ʱ����P��ͼ��G������ɵ��������磬��P����1��0����ֱ��y��x������ɵ�����
��֪��O�İ뾶Ϊ1��ֱ��l��y����x+b��
��1����b����3ʱ��
����O��0��0����A����4��1����B����4����1�������У���ֱ��l������ɵ������ǣ�_____��
����ֱ��l�ϵĵ�M��m��n���ǡ�O������ɵ�������m��ȡֵ��Χ��
��2����P��ֱ��l�ϣ��ҵ�P�ǡ�O������ɵ��������������������ĵ�P����һ�����Ȳ�Ϊ0���߶Σ���ֱ��д��b��ȡֵ��Χ��

���𰸡���1����A��B���ک�4��m����2��1��m��1����2����2��b��![]() ��
��
��������
��1���ٸ�������ɵ����Ķ��弴�ɽ�����⣮
�ڹ��㣨0��1���͵㣨0����1����x���ƽ���߷ֱ�ֱ��l��M1��M2�����㣨1��0���͵㣨��1��0����y���ƽ���߷ֱ�ֱ��l��M3��M4���ɴ˼����жϣ�
��2����M2��M3�غϣ�����Ϊ����1����1��ʱ����1��1+b���ɵ�b����2����ֱ��l���O����ʱ�����е�ΪE����y����F�������E�����꣬�����жϣ�
��1���١�b����3ʱ��ֱ��l��y����x��3��
��ֱ��l��x��Ľ���Ϊ������3��0����ֱ��l��y��Ľ���Ϊ����0����3����
��O��0��0����ֱ��l���Ϸ���
��O��0��0������ֱ��l������ɵ�����
�ߵ�x����4ʱ��y��4��3��1��
���A����4��1����ֱ��l�ϣ�
���A��ֱ��l������ɵ�����
�ߵ�B����4����1����ֱ��l���·����ѵ�B����4����1������ƽ��2�����ȵ�λΪ����4��1����
���B��ֱ��l������ɵ�����
�ʴ�Ϊ��A��B��
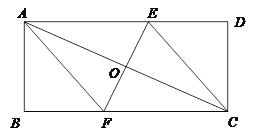
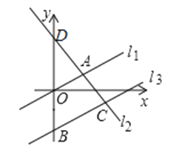
����ֱ��l��y����x��3���ֱ���ֱ��y��1��y����1��x����1��x��1���ν��ڵ�M1��M2��M3��M4����ͼ1��ʾ��
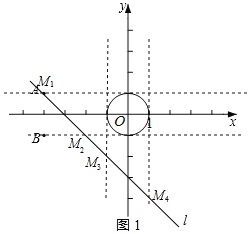
���M1��M2��M3��M4�ĺ�����ֱ�Ϊ��4����2����1��1��
�߶�M1M2�ϵĵ����ҵķ���ƽ�����O���ཻ���߶�M3M4�ϵĵ����ϵķ���ƽ�����O���ཻ��
���߶�M1M2���߶�M3M4�ϵĵ��ǡ�O������ɵ�����
��m��ȡֵ��Χ�ǩ�4��m����2��1��m��1��
��2����ͼ2��ʾ��
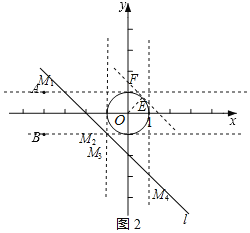
��M2��M3�غϣ�����Ϊ����1����1��ʱ����1��1+b����b����2��
�ڵ�ֱ��l���O����ʱ�����е�ΪE����y����F��
�����⣬��Rt��OEF�У���OEF��90����OE��1����EOF��45����
���OEF�ǵ���ֱ�������Σ�
��OF��![]() OE��
OE��![]() ��
��
�۲�ͼ���֪����������b��ֵΪ��2��b��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij�̵����һ����Ʒ�����г����鷴ӳ������Ʒ����������y�����������۵���x��Ԫ��֮������һ�κ�����ϵ�����ڸ���Ʒ�����۵��ۣ���������������������IJ��ֶ�Ӧ���������[ע���������������������������۵��۩��ɱ����ۣ�
���۵���x��Ԫ�� | 75 | 78 | 82 |
��������y������ | 150 | 120 | 80 |
����������w��Ԫ�� | 5250 | a | 3360 |
��1������������Ϣ����գ��ò�Ʒ�ijɱ��������� ��Ԫ������a��ֵ���� ����y����x�ĺ�����ϵʽ���� ����
��2�������Ʒ��������������ֵ��
��3������ij��ԭ����Ʒ���۽�����mԪ/����m��0�������̵��ڽ��������У��̵�涨����Ʒ�����۵��۲�����68Ԫ���������������۵�����Ȼ���㣨1���еĺ�����ϵ�������������������6600Ԫ��ֱ��д��m��ֵ��