题目内容
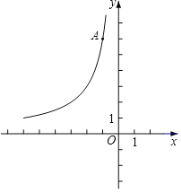
【题目】如图，在平面直角坐标系xOy中，函数y＝
（x＜0）的图象经过点A（﹣1，6）．
（1）求k的值；
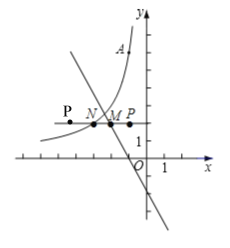
（2）已知点P（a，﹣2a）（a＜0），过点P作平行于x轴的直线，交直线y＝﹣2x﹣2于点M，交函数y＝（x＜0）的图象于点N．
①当a＝﹣1时，求线段PM和PN的长；
②若PN≥2PM，结合函数的图象，直接写出a的取值范围．
【答案】（1）k=-6；（2）①PM＝1，PN＝2；②a≤﹣3或﹣1≤a＜0．
【解析】
（1）把点A（﹣1，6）代入解析式即可求解；
（2）①当a＝﹣1时，点P的坐标为（﹣1，2），把y＝2分别代入y＝﹣2x﹣2与y＝﹣
即可求得M、N的坐标，进一步即可求得PM、PN；
②先求出PN＝2PM时a的值，再根据函数的图象即可求解．
（1）∵函数y＝
（x＜0）的图象经过点A（﹣1，6）．
∴k＝﹣1×6＝﹣6．
（2）①当a＝﹣1时，点P的坐标为（﹣1，2）．
∵直线y＝﹣2x﹣2，反比例函数的解析式为y＝﹣，PN∥x轴，
∴把y＝2代入y＝﹣2x﹣2，求得x＝﹣2，代入y＝﹣求得x＝﹣3，
∴M（﹣2，2），N（﹣3，2），
∴PM＝1，PN＝2．
②把y＝-2a代入y＝﹣2x﹣2，求得x＝a-1；代入y＝﹣求得x＝
，
∴M点的坐标为(a-1，-2a)，N点的坐标为(，-2a)
当PN＝2PM时，
，解得：a=±1或±3（负值舍去）
∴当a＝﹣1或a＝﹣3时，PN＝2PM，
∴根据图象PN≥2PM，a的取值范围为a≤﹣3或﹣1≤a＜0．
【题目】为了解早高峰期间A，B两邻近地铁站乘客的乘车等待时间（指乘客从进站到乘上车的时间），某部门在同一上班高峰时段对A、B两地铁站各随机抽取了500名乘客，收集了其乘车等待时间（单位：分钟）的数据，统计如表：
等待时的频数间 乘车等待时间 地铁站 | 5≤t≤10 | 10＜t≤15 | 15＜t≤20 | 20＜t≤25 | 25＜t≤30 | 合计 |
A | 50 | 50 | 152 | 148 | 100 | 500 |
B | 45 | 215 | 167 | 43 | 30 | 500 |
据此估计，早高峰期间，在A地铁站“乘车等待时间不超过15分钟”的概率为_____；夏老师家正好位于A，B两地铁站之间，她希望每天上班的乘车等待时间不超过20分钟，则她应尽量选择从_____地铁站上车．（填“A”或“B”）
