题目内容
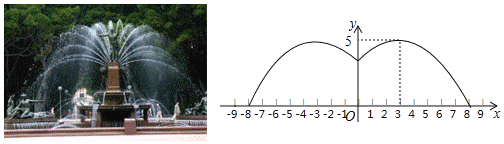
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的
轴的![]() 个交点坐标为
个交点坐标为![]() ,
,![]() ,其部分图象如图所示,下列结论:①
,其部分图象如图所示,下列结论:①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
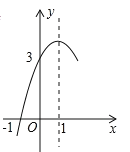
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的另个交点坐标为(3,0),则可对②进行判断;由对称轴方程可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断.
∵观察函数的图象知:抛物线与![]() 轴有2个交点,
轴有2个交点,
∴![]() >0,所以①错误;
>0,所以①错误;
∵抛物线的对称轴为直线![]() ,
,
而点![]() 关于直线
关于直线![]() 的对称点的坐标为
的对称点的坐标为![]() ,
,
∴方程![]() 的两个根是
的两个根是![]() ,所以②正确;
,所以②正确;
∵抛物线的对称轴为![]() ,即
,即![]() ,
,
∴![]() ,所以③正确;
,所以③正确;
∵抛物线与![]() 轴的两点坐标为
轴的两点坐标为![]() ,
,![]() ,且开口向下,
,且开口向下,
∴当y>0时,![]() 的取值范围是
的取值范围是![]() ,所以④正确;
,所以④正确;
综上,②③④正确,正确个数有3个.
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?