题目内容
【题目】甲开车从距离B市100千米的A市出发去B市,乙从同一路线上的C市出发也去往B.市,二人离A市的距离与行驶时间的函数图像如图所示(y代表距离,x代表时间)
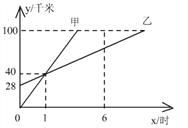
(1)C市离A市的距离是_________千米;
(2)甲的速度是________千米∕小时,乙的速度是___________千米∕小时;
(3)________小时,甲追上乙;
(4)试分别写出甲、乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式.
【答案】(1)28;(2)40,12;(3)1;(4)甲:y=40x,乙:y=12x+28.
【解析】
(1)由函数图象可以直接得出C市离A市的距离是28千米;
(2)由函数图象可以直接得出甲的速度为40千米∕小时,乙的速度为12千米∕小时;(3)由函数图象可以直接得出1小时,甲追上乙;
(4)设甲离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为y甲=![]() x,乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为y乙=
x,乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为y乙=![]() x+b,由待定系数法求出其解即可.
x+b,由待定系数法求出其解即可.
解:(1)由函数图象可以直接得出C市离A市的距离是28千米.
故答案为28;
(2)由函数图象可以直接得出甲的速度为40千米∕小时,乙的速度为12千米∕小时.
故答案为40,12;
(3)由函数图象可以直接得出1小时,甲追上乙.
故答案为1;
(4)设甲离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为:![]() =
=![]() x,乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为:
x,乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式为:![]() =
=![]() x+b,由题意,得40=
x+b,由题意,得40=![]() ,∴
,∴![]() =40x(0≤x≤2.5) .
=40x(0≤x≤2.5) .
由![]() ,解得:
,解得:![]() ,
,
∴![]() =12x+28(0≤x≤6) .
=12x+28(0≤x≤6) .

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
出厂价 | 成本价 | 排污处理费 | |
甲种塑料 | 2100(元/吨) | 800(元/吨) | 200(元/吨) |
乙种塑料 | 2400(元/吨) | 1100(元/吨) | 100(元/吨) 另每月还需支付设备管理、维护费20000元 |
(1)设该车间每月生产甲、乙两种塑料各x吨,利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨时,获得的总利润最大?最大利润是多少?