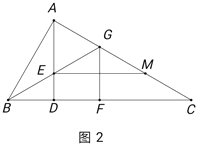
题目内容
【题目】如图,在菱形ABCD中,∠![]() =∠EAF=
=∠EAF=![]() ,∠BAE=
,∠BAE=![]() ,则∠CEF=________.
,则∠CEF=________.

【答案】20°
【解析】
首先证明△ABE≌△ACF,然后推出AE=AF,证明△AEF是等边三角形,得∠AEF=60°,最后求出∠CEF的度数.
解:连接AC, 在菱形ABCD中,AB=CB, ∵![]() =60°,
=60°,
∴∠BAC=60°,△ABC是等边三角形,
∵∠EAF=60°, ∴∠BAC-∠EAC=∠EAF-∠EAC,
即:∠BAE=∠CAF,
在△ABE和△ACF中,
 ,
,
∴△ABE≌△ACF(ASA),
∴AE=AF, 又∠EAF=∠D=60°,
则△AEF是等边三角形, ∴∠AEF=60°,
又∠AEC=∠B+∠BAE=80°,
则∠CEF=80°-60°=20°.
故答案为:20°.


练习册系列答案
相关题目