题目内容
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
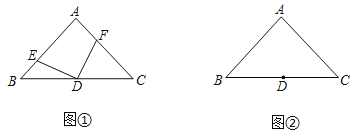
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF.
①求证:BE=AF;
②若S△BDE=![]() S△ABC=2,求S△CDF;
S△ABC=2,求S△CDF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF.
①BE=AF还成立吗?请利用图②说明理由;
②若S△BDE=![]() S△ABC=8,直接写出DF的长.
S△ABC=8,直接写出DF的长.
【答案】(1)①证明见解析;②S△DFC=4;(2)①结论成立.理由见解析;②DF=4![]() .
.
【解析】
(1)①只要证明△BDE≌△ADF(ASA)可得结论.
②求出△ADC,△ADF的面积即可解决问题.
(2)①结论成立,证明方法类似(1).
②利用三角形的面积公式求出AB,再证明AB=2BE,求出DH,EH,利用勾股定理求出DE即可解决问题.
(1)①证明:如图①中,连接AD.
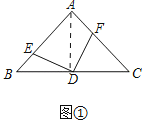
∵AB=AC,∠BAC=90°,BD=DC,
∴AD⊥BC,AD=BD=CD,∠B=∠C=∠DAC=45°,
∵∠EDF=∠BDA=90°,
∴∠BDE=∠ADF,
∴△BDE≌△ADF(ASA),
∴BE=DF.
②解:∵S△BDE=![]() S△ABC=2,
S△ABC=2,
∴S△BDE=2,S△ABC=12,
∵BD=DC,
∴S△ADC=![]() S△ADC=6,
S△ADC=6,
∵△BDE≌△ADF,
∴S△ADF=S△BDE=2,
∴S△DFC=6﹣2=4.
(2)①证明:结论成立.
理由:如图②中,
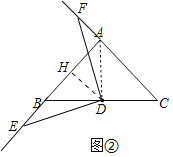
∵AB=AC,∠BAC=90°,BD=DC,
∴AD⊥BC,AD=BD=CD,∠B=∠C=∠DAC=45°,
∵∠EDF=∠BDA=90°,
∴∠BDE=∠ADF,
∴△BDE≌△ADF(ASA),
∴BE=DF.
②解:如图②中,作DH⊥AB于H.
∵S△BDE=![]() S△ABC=8,
S△ABC=8,
∴S△ABC=32,
∴![]() AB2=32,
AB2=32,
∴AB=AC=8,BC=8![]() ,DH=
,DH=![]() AB=4,
AB=4,
∵BD=DC,
∴S△ABD=S△ADC,
∴S△BDE=![]() S△ADB,
S△ADB,
∴AB=2BE,
∴BE=BH=AH=4,
∴![]() ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案