ЬтФПФкШн
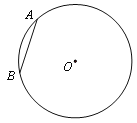
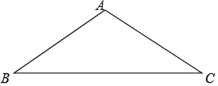
ЁОЬтФПЁПЃЈ1ЃЉЗЂЯжЃКШчЭМ1ЃЌЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧвBCЃНaЃЌABЃНbЧвЛиД№ЃКЕБЕуAЮЛгкФЧЬѕЯпЖЮЕФбгГЄЯпЩЯЪБЃЌЯпЖЮACЕФГЄШЁЕУзюДѓжЕЃЌЧвзюДѓжЕЮЊЖрЩйЃЈгУКЌaЁЂbЕФЪНзгБэЪОЃЉЃЎ
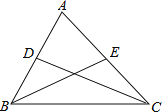
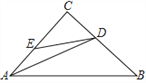
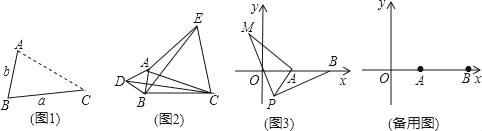
ЃЈ2ЃЉгІгУЃКЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧвBCЃН4ЃЌABЃН2ЃЌШчЭМ2ЫљЪОЃЌЗжБ№вдABЃЌACЮЊБпЃЌзїЕШБпШ§НтаЮABDКЭЕШБпШ§НЧаЮACEЃЌСЌНгCDЃЌBEЃЎЂйЧыевГіЭМжагыBEЯрЕШЕФЯпЖЮЃЌВЂЫЕУїРэгЩЃЛЂкжБНгаДГіЯпЖЮBEГЄЕФзюДѓжЕЃЎ
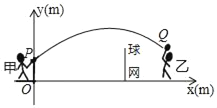
ЃЈ3ЃЉЭиеЙЃКШчЭМ3ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ5ЃЌ0ЃЉЃЌЕуPЮЊЯпЖЮABЭтвЛЖЏЕуЃЌЧвPAЃН2ЃЌPMЃНPBЃЌЁЯBPMЃН90ЁуЃЌЧыжБНгаДГіЯпЖЮAMГЄЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉCBЃЌa+bЃЛЃЈ2ЃЉЂйCDЃНBEЃЌРэгЩМћНтЮіЃЛЂкзюДѓжЕЮЊ4ЃЛЃЈ3ЃЉТњзуЬѕМўЕФЕуPзјБъЃЈ2Љ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ2Љ
ЃЉЛђЃЈ2Љ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌAMЕФзюДѓжЕЮЊ2
ЃЉЃЌAMЕФзюДѓжЕЮЊ2![]() +3ЃЎ
+3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуAЮЛгкCBЕФбгГЄЯпЩЯЪБЃЌЯпЖЮACЕФГЄШЁЕУзюДѓжЕЃЌМДПЩЕУЕННсТл
ЃЈ2ЃЉЂйИљОнЕШБпШ§НЧаЮЕФаджЪЕУЕНAD=ABЃЌAC=AEЃЌЁЯBAD=ЁЯCAE=60ЁуЃЌЭЦГіЁїCADЁеЁїEABЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНCD=BEЃЛЂкгЩгкЯпЖЮBEГЄЕФзюДѓжЕ=ЯпЖЮCDЕФзюДѓжЕЃЌИљОнЃЈ1ЃЉжаЕФНсТлМДПЩЕУЕННсЙћЃЛ
ЃЈ3ЃЉСЌНгBMЃЌНЋЁїAPMШЦзХЕуPЫГЪБеыа§зЊ90ЁуЕУЕНЁїPBNЃЌСЌНгANЃЌЕУЕНЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНPN=PA=2ЃЌBN=AMЃЌИљОнЕБNдкЯпЖЮBAЕФбгГЄЯпЪБЃЌЯпЖЮBNШЁЕУзюДѓжЕЃЌМДПЩЕУЕНзюДѓжЕЮЊ2![]() +3ЃЛЙ§PзїPEЁЭxжсгкEЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌМДПЩЕУЕНPЕуЕФвЛИізјБъЃЌдйИљОнЖдГЦадЕУЕНPЕуЕФСэЭтвЛИізјБъМДПЩЕУГіД№АИ
+3ЃЛЙ§PзїPEЁЭxжсгкEЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌМДПЩЕУЕНPЕуЕФвЛИізјБъЃЌдйИљОнЖдГЦадЕУЕНPЕуЕФСэЭтвЛИізјБъМДПЩЕУГіД№АИ
ЃЈ1ЃЉЁпЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌЧвBCЃНaЃЌABЃНbЃЌ
ЁрЕБЕуAЮЛгкCBЕФбгГЄЯпЩЯЪБЃЌЯпЖЮACЕФГЄШЁЕУзюДѓжЕЃЌЧвзюДѓжЕЮЊBC+ABЃНa+bЃЌ
ЃЈ2ЃЉЂйCDЃНBEЃЌ
РэгЩЃКЁпЁїABDгыЁїACEЪЧЕШБпШ§НЧаЮЃЌ
ЁрADЃНABЃЌACЃНAEЃЌЁЯBADЃНЁЯCAEЃН60ЁуЃЌ
ЁрЁЯBAD+ЁЯBACЃНЁЯCAE+ЁЯBACЃЌ
МДЁЯCADЃНЁЯEABЃЌ
дкЁїCADгыЁїEABжаЃЌ
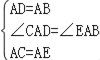 ЃЌ
ЃЌ
ЁрЁїCADЁеЁїEABЃЌ
ЁрCDЃНBEЃЛ
ЂкЁпЯпЖЮBEГЄЕФзюДѓжЕЃНЯпЖЮCDЕФзюДѓжЕЃЌ
гЩЃЈ1ЃЉжЊЃЌЕБЯпЖЮCDЕФГЄШЁЕУзюДѓжЕЪБЃЌЕуDдкCBЕФбгГЄЯпЩЯЃЌ
ЁрзюДѓжЕЮЊBD+BCЃНAB+BCЃН4ЃЛ
ЃЈ3ЃЉСЌНгBMЃЌЁпНЋЁїAPMШЦзХЕуPЫГЪБеыа§зЊ90ЁуЕУЕНЁїPBNЃЌСЌНгANЃЌ

дђЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPNЃНPAЃН2ЃЌBNЃНAMЃЌ
ЁпAЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ5ЃЌ0ЃЉЃЌ
ЁрOAЃН2ЃЌOBЃН5ЃЌ
ЁрABЃН3ЃЌ
ЁрЯпЖЮAMГЄЕФзюДѓжЕЃНЯпЖЮBNГЄЕФзюДѓжЕЃЌ
ЁрЕБNдкЯпЖЮBAЕФбгГЄЯпЪБЃЌЯпЖЮBNШЁЕУзюДѓжЕЃЌ
зюДѓжЕЃНAB+ANЃЌ
ЁпANЃН![]() APЃН2
APЃН2![]() ЃЌ
ЃЌ
ЁрзюДѓжЕЮЊ2 ![]() +3ЃЛ
+3ЃЛ
ШчЭМ2ЃЌЙ§PзїPEЁЭxжсгкEЃЌ

ЁпЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPEЃНAEЃН![]() ЃЌ
ЃЌ
ЁрOEЃНBOЉABЉAEЃН5Љ3Љ![]() ЃН2Љ
ЃН2Љ![]() ЃЌ
ЃЌ
ЁрPЃЈ2Љ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ШчЭМ3жаЃЌ
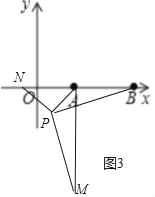
ИљОнЖдГЦадПЩжЊЕБЕуPдкЕкЫФЯѓЯоЪБЃЌPЃЈ2Љ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЪБЃЌвВТњзуЬѕМўЃЎ
ЃЉЪБЃЌвВТњзуЬѕМўЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуPзјБъЃЈ2Љ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ2Љ
ЃЉЛђЃЈ2Љ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌAMЕФзюДѓжЕЮЊ2
ЃЉЃЌAMЕФзюДѓжЕЮЊ2![]() +3ЃЎ
+3ЃЎ

 ПьНнгЂгяжмжмСЗЯЕСаД№АИ
ПьНнгЂгяжмжмСЗЯЕСаД№АИ