题目内容
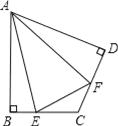
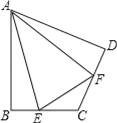
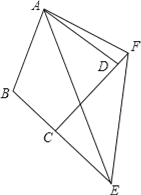
【题目】如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC=![]() (AB+AE);④ S△ADC=
(AB+AE);④ S△ADC=![]() S四边形ABDE,其中正确的结论个数为( )
S四边形ABDE,其中正确的结论个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
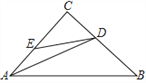
【解析】在AB上截取AF=AE,交AB于点F,如图所示:
∵AD是∠CAB的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
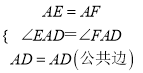 ,
,
∴△AED≌△AFD(SAS),
∴∠DEA=∠DFA,DF=DE,
又∵DE=DB,
∴DF=DB,
∴∠DFB=∠B,
又∵∠DFA+∠DFB=180o,∠DEA=∠DFA,
∴∠DEA+∠B=180°(等量代换),
又∵∠CED+∠AED=180o,
∴∠CED=∠B,
又∵∠C+∠CED+∠CDE=180o,∠C+∠CAB+∠B=180o,
∴∠CDE=∠CAB,
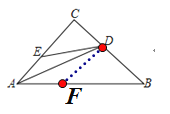
过点D作DG![]() AB于点G,如图所示:
AB于点G,如图所示:
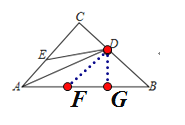
∵DG=DB(已证),
∴DG是BF的垂直平分线,
∴FG=BG,
∵AD是是∠CAB的角平分线,∠C=90°,DG![]() AB,
AB,
∴DC=DG,
在△ADC和△AGD中
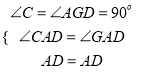 ,
,
∴△ADC≌△AGD(AAS),
∴AC=AG,
又∵AC=AE+CE,AG=AF+FG,
∴AE+CE=AF+FG,
又∵AE=AF,
∴CE=FG,
又∵FG=BG,
∴CE=BG,
∴AC=AE+BG,
又∵AB+AE=AG+BG+AE,AG=AC,
∴AB+AE=AC+AC=2AC,即AC=![]() (AB+AE),
(AB+AE),
∵S四边形ABDE=S△ABD+S△AED=![]() ,
,
∴S四边形ABDE ![]() ,
,
又∵S△ADC=![]() ,
,
∴S△ADC=![]() S四边形ABDE.
S四边形ABDE.
故①②③④都正确,共计4个正确.
故选A.

【题目】在中考体育加试中,某班30名男生的跳远成绩如下表:
成绩/m | 1.95 | 2.00 | 2.05 | 2.10 | 2.15 | 2.25 |
人数 | 2 | 3 | 9 | 8 | 5 | 3 |
这些男生跳远成绩的众数、中位数分别是( )
A. 2.10,2.05B. 2.10,2.10C. 2.05,2.10D. 2.05,2.05