Question

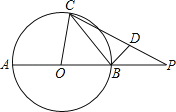
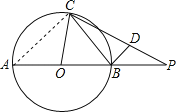
【题目】如图，AB是⊙O的直径，延长AB至P，使BP=OB，BD垂直于弦BC，垂足为点B，点D在PC上．设∠PCB=α，∠POC=2β．求证：tanαtanβ=．

Answer 1

【答案】见解析

【解析】

试题分析：首先连接AC，易得∠A=β，由AB是⊙O的直径，可表示出tanβ，又由BD垂直于弦BC，可表示出tanα，BD∥AC，证得△PBD∽△PAC，然后由相似三角形的对应边成比例，求得答案．

证明：连接AC，则∠A=∠POC=β，

∵AB是⊙O的直径，

∴∠ACB=90°，

∴tanβ=，

∵BD垂直于弦BC，

即DB⊥BC，

∴tanα=，BD∥AC，

∴tanatanβ==，

∴∠DBP=∠A，

又∵∠P=∠P，

∴△PBD∽△PAC，

∴=，

∵PB=0B=OA，

∴=，

∴tanatanβ=．