题目内容
【题目】在Rt△ABC中,BC=4,AC=8,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
(1)若PD⊥AB,求AP;
(2)若△PDE与△ABC重合部分的面积等于△PAB面积的![]() ,求AP的长.
,求AP的长.
【答案】(1)AP=5;(2)AP=6或2![]() .
.
【解析】
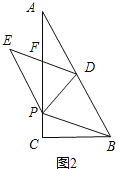
试题分析:(1)如图1,根据勾股定理可求出AB,从而得到AD、BD的值,易证△ADP∽△ACB,只需运用相似三角形的性质就可求出AP的值;
(2)根据条件可得S△PDF=![]() S△PAB=
S△PAB=![]() S△ADP=
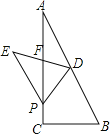
S△ADP=![]() S△EDP,从而可得AF=PF,EF=DF.而符合条件的位置有两个(图3、图4),需分两种情况讨论:①如图3,根据三角形中位线定理可得DF∥BP,则有∠EDP=∠BPD.由折叠可得∠BDP=∠EDP,从而可得∠BDP=∠BPD,即可得到BP=BD=2
S△EDP,从而可得AF=PF,EF=DF.而符合条件的位置有两个(图3、图4),需分两种情况讨论:①如图3,根据三角形中位线定理可得DF∥BP,则有∠EDP=∠BPD.由折叠可得∠BDP=∠EDP,从而可得∠BDP=∠BPD,即可得到BP=BD=2![]() ,在Rt△BCP中运用勾股定理可求出PC,就可得到AP的值;②如图4,连接AE,由AF=PF,EF=DF可得四边形AEDP是平行四边形,则有AP=ED,由折叠可得DE=DB,即可得到AP=DB=2
,在Rt△BCP中运用勾股定理可求出PC,就可得到AP的值;②如图4,连接AE,由AF=PF,EF=DF可得四边形AEDP是平行四边形,则有AP=ED,由折叠可得DE=DB,即可得到AP=DB=2![]() .
.
解:(1)如图:∵∠C=90°,BC=4,AC=8,
∴AB=4![]()
∵点D为AB的中点,
∴AD=DB=2![]()
∵PD⊥AB,
∴∠ADP=90°,
∵∠A=∠A,∠ADP=∠C,
∴△ADP∽△ACB,
∴![]() ,
,
∴AP=5;
(2)∵点D是线段AB的中点,
∴S△ADP=S△BDP=S△PAB.
由折叠可得:S△EDP=S△BDP,
∴S△PDF=![]() S△PAB=
S△PAB=![]() S△ADP=
S△ADP=![]() S△EDP,
S△EDP,
∴AF=PF,EF=DF.
①如图3,
根据三角形中位线定理可得:DF∥BP,
∴∠EDP=∠BPD.
由折叠可得∠BDP=∠EDP,
∴∠BDP=∠BPD,
∴BP=BD=2![]() ,
,
∴PC=![]() ,
,
∴AP=8﹣2=6;
②如图4,
连接AE,
∵AF=PF,EF=DF,
∴四边形AEDP是平行四边形,
∴AP=ED,
由折叠可得:DE=DB,
∴AP=DB=2![]() .
.
综上所述:AP=6或2![]() .
.