��Ŀ����
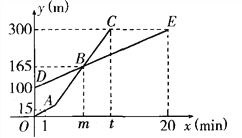
����Ŀ��Сǿ�Ͱְ���ɽ���棬���˾����ĸ߶�y(m)��Сǿ��ɽʱ��x(min)֮��ĺ���ͼ��ֱ���ͼ������OAC(Сǿ)���߶�DE(�ְ�)��ʾ�����ݺ���ͼ���������̽����
(1)�ְֵ�ɽ���ٶ���ÿ����_______m��
(2)�����ͼ�е�B��ʵ�����壻
(3)���߶�DE����ʾ��y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(4)��m��ֵ��
(5)��Сǿ���ٺ�����ɽ���ٶ��ǰְ��ٶȵ�3��������Сǿ��ɽ�ʱ��ʱ��ʼ���٣���ʱСǿ�����ĸ߶��Ƕ����ף�
���𰸡���1��10����2��(2) B�����壺�����߶�Ϊ165mʱ������������Сǿ�ϰְ֣�����3��y=10x+100(0��x��20)��4��6.5����5��Сǿ��ɽ2 minʱ��ʼ���٣���ʱСǿ�����ĸ߶���30 m.
������������:(1)�ðְֵ�ɽ�ĸ߶ȡµ�ɽ�õ�ʱ�䣬�Ϳ�������ְֵ�ɽ���ٶȣ�
(2)��ʾСǿ�Ͱְ��ڸ߶�Ϊ165�ĵط�������
(3)���߶�DE����(0��100)��(20��300)���㣬ֱ���ô���ϵ�����Ϳ���ֱ����������ʽ��������ȷ���Ա�����ȡֵ��Χ��
(4)��y=165�����߶�DE�Ľ���ʽ�Ϳ������x��ֵ����m��ֵ��
(5)���������֪��Сǿ�ڵ���165��300�����õ�ʱ����t��m�������Ϳ������ٶȵĹ�ϵ����������ϵ�Ϳ���t��ֵ�����C�Ľ���ʽ���ô���ϵ�����Ϳ������BC�Ľ���ʽ�������OA�Ľ���ʽ�������������ֱ�ߵĽ�������Ϳ����������.
�� (1)10
(2) B�����壺�����߶�Ϊ165mʱ������������Сǿ�ϰְ֣���
(3) ��DE��Ӧһ�κ���Ϊy=kx+b
��D��0��100�� E��20,300��
��![]()
��![]()
��y=10x+100(0��x��20)
(4)��B(m,165)����y=10x+100��m=6.5
(5) �ְֵ߰��ٶ�v=![]() =10m/min
=10m/min
��Сǿ���ٺ���ٶ�3v=30m/min
��t-m=![]() 4.5
4.5
��C(11,300) 10
��BC��Ӧһ�κ���Ϊy=30x-30
��OA��Ӧһ�κ���Ϊy=15x
��A��������2,30��
��Сǿ��ɽ2 minʱ��ʼ���٣���ʱСǿ�����ĸ߶���30 m
�㾦: ������һ��һ�κ������ۺ����⣬�������ٶ�=·�̡�ʱ������ã����⺯��ͼ������壬����ϵ���������Ľ���ʽ�����ã�������Ľⷨ�ȶ��֪ʶ��.����ж���ͼ��������ǹؼ�.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ����һ�������Ŀڴ���װ�����ɸ���ͬ�ĺ���Ϊ�˹��ƴ��к����������ijѧϰС����������ʵ�飬���ǽ�30��������С��״��ȫ��ͬ�İ���װ����У����Ⱥ�����������һ��������ɫ���ٰ����Żش��У������ظ����±��Ǽ��λ���ܺ�ͳ�Ƶ����ݣ�
����Ĵ���s | 150 | 200 | 500 | 900 | 1000 | 1200 |
���������Ƶ��n | 51 | 64 | 156 | 275 | 303 | 361 |
���������Ƶ�� | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
��1������ƣ�������s�ܴ�ʱ�����������Ƶ�ʽ���ӽ��� ����������ȥ��һ�Σ�����������ĸ������� ������ȷ��0.1����
��2���Թ���ڴ��к����ж���ֻ��
��3����������������������ͳ������ʷ���̸һ����ʾ��