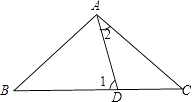Question

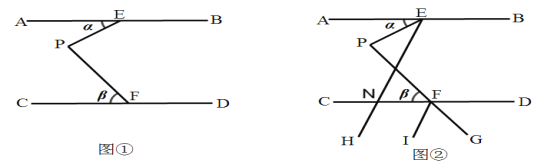
【题目】已知：如图1，过等腰直角三角形ABC的直角顶点A作直线AP，点B关于直线AP的对称点为E，连接BE，CE，其中CE交直线AP于点F．

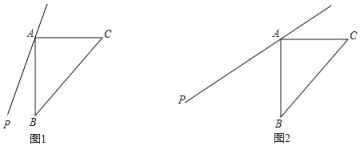
（1）依题意补全图形；

（2）若∠PAB＝16°，求∠ACF的度数；

（3）如图2，若45°＜∠PAB＜90°，用等式表示线段AB，FE，FC之间的数量关系，并证明．

Answer 1

【答案】（1）详见解析；（2）29°；（3）FE2+FC2＝2AB2

【解析】

（1）根据题意补全图形；

（2）连接AE，根据轴对称的性质和等腰直角三角形的性质，可得AE＝AB，∠EAP＝∠BAP＝16°，AE＝AC＝AB，根据三角形的内角和可求∠ACF的度数；

（3）连接AE，BF，设BF交AC于点G，根据轴对称的性质可得AE＝AB，FE＝FB，可证△AEF≌△ABF，可得∠FEA＝∠FBA，根据等腰三角形的性质可得∠ACE＝∠ABF，即可求∠CFB＝∠BAC＝90°，根据勾股定理可得线段AB，FE，FC之间的数量关系．

解：（1）补全图形，如图所示．

（2）如图，连接AE，

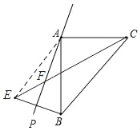
∵点E与点B关于直线AP对称，

∴对称轴AP是EB的垂直平分线．

∴AE＝AB，∠EAP＝∠BAP＝16°，

∵等腰直角三角形ABC，

∴AB＝AC，∠BAC＝90°，

∴AE＝AC，

∴∠AEC＝∠ACF

∴2∠ACF+32°+90°＝180°，

∴∠ACF＝29°，

（3）AB，FE，FC满足的数量关系：FE2+FC2＝2AB2，

理由如下：连接AE，BF，设BF交AC于点G，

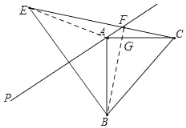
∵点E与点B关于直线AP对称，

∴对称轴AP是EB的垂直平分线，

∴AE＝AB，FE＝FB，

又∵AF＝AF，

∴△AEF≌△ABF（SSS），

∴∠FEA＝∠FBA，

∵AB＝AC，

∴AE＝AC，

∴∠ACE＝∠AEC，

∴∠ACE＝∠ABF，

又∵∠CGF＝∠AGB，

∴∠CFB＝∠BAC＝90°，

∴FB2+FC2＝BC2．

∵BC2＝2AB2，

∴FE2+FC2＝2AB2