题目内容
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.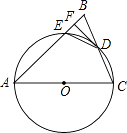
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
【答案】
(1)证明:如图,
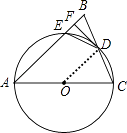
连接OD.
∵AB=AC,
∴∠B=∠C,
∵OD=OC,
∴∠ODC=∠C,
∴∠ODC=∠B,
∴OD∥AB,
∵DF⊥AB,
∴OD⊥DF,
∵点D在⊙O上,
∴直线DF与⊙O相切;
(2)解:∵四边形ACDE是⊙O的内接四边形,
∴∠AED+∠ACD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠ACD,
∵∠B=∠B,
∴△BED∽△BCA,
∴ ![]() =
= ![]() ,
,
∵OD∥AB,AO=CO,
∴BD=CD= ![]() BC=3,
BC=3,
又∵AE=7,
∴ ![]() =
= ![]() ,
,
∴BE=2,
∴AC=AB=AE+BE=7+2=9.
【解析】(1)连接OD,利用AB=AC,OD=OC,证得OD∥AD,再证明DF⊥OD,即查得到DF为⊙O的切线;
(2)四边形ACDE是⊙O的内接四边形,∠BED=∠ACD,∠B=∠B,证得△BED∽△BCA,再由相似三角形的性质求得BE的值,最后即可求得AC的长.
【考点精析】本题主要考查了切线的判定定理和相似三角形的判定与性质的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受人们的喜欢,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,2016年经过改造升级后A型车每辆销售价比2015年增加400元,若2016年6月份与2015年6月份卖出的A型车数量相同,则2016年6月份A型车销售总额将比2015年6月份销售总额增加25%.
(1)求2016年6月份A型车每辆销售价为多少元(用列方程的方法解答);
(2)该车行计划2016年7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格/(元/辆) | 1100 | 1400 |
销售价格/(元/辆) | 2016年的销售价格 | 2400 |
应如何进货才能使这批车获利最多?