��Ŀ����
����Ŀ��[��֪]
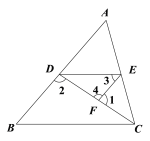
��ͼ�٣���ABC�ǵȱ������Σ�D�DZ�BC��һ�㣨��D�����B��C�غϣ�������EDF=60�㣬ʹ�ǵ����߷ֱ�AB��AC�ڵ�E��F����BD=CF����DE��BC�����DFC�Ĵ�С���� ���ȣ�
[̽��]
��ͼ�ڣ���ABC�ǵȱ������Σ�D�DZ�BC��һ�㣨��D�����B��C�غϣ�������EDF=60�㣬ʹ�ǵ����߷ֱ�AB��AC�ڵ�E��F����BD=CF����֤��BE=CD��
[Ӧ��]
��ͼ���У���D�DZ�BC���е㣬��AB=2�������������䣬��ͼ����ʾ�����ı���AEDF���ܳ�Ϊ�� ����
���𰸡���1��90����2�������������3��4
��������
[��֪]�ɵȱ�����������֪��B=��C=60�㣬����DE��BC����EDF=60��֪��BED=��CDF=30�㣬�ݴ˿ɵô𰸣�
[̽��]�ɡ�EDF+��CDF=��B+��BED���ҡ�EDF=��B=60��֪��CDF=��BED���ݴ�֤��BDE�ա�CFD�ɵô𰸣�
[Ӧ��]�ȵó�BD=CD=CF=AF=1������[̽��]֪��BDE�ա�CFD���ݴ˵�BE=CD=1��DE=DF����ϡ�B=60��֪��BDE�ǵȱ������Σ��ó�DE=DF=1���ٽ�һ�����ɵô𰸣�
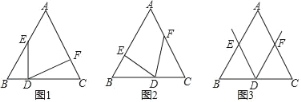
[��֪]��ͼ1��
�ߡ�ABC�ǵȱ������Σ����B=��C=60�㣮
��DE��BC������BDE=90�㣬��EDF=60�㣬���BED=��CDF=30�㣬���DFC=90�㣮
�ʴ�Ϊ��90��
[̽��]�ߡ�ABC�ǵȱ������Σ����B=��C=60�㣮
�ߡ�EDF+��CDF=��B+��BED���ҡ�EDF=60�㣬���CDF=��BED��
�ڡ�BDE�͡�CFD�У���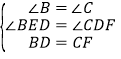 �����BDE�ա�CFD��AAS������BE=CD��
�����BDE�ա�CFD��AAS������BE=CD��
[Ӧ��]�ߡ�ABC�ǵȱ������Σ�AB=2�����B=��C=60�㣬AB=BC=AC=2��
��DΪBC�е㣬��BD=CF����BD=CD=CF=AF=1����[̽��]֪��BDE�ա�CFD����BE=CD=1��DE=DF��
�ߡ�B=60�㣬���BDE�ǵȱ������Σ���DE=DF=1�����ı���AEDF���ܳ�ΪAE+DE+DF+AF=4��
�ʴ�Ϊ��4��

 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�