Question

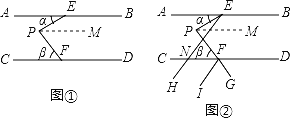
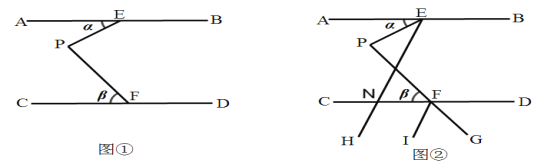
【题目】如图①，已知AB∥CD，点E、F分别是AB、CD上的点，点P是两平行线之间的一点，设∠AEP=α，∠PFC=β，在图①中，过点E作射线EH交CD于点N，作射线FI，延长PF到G，使得PE、FG分别平分∠AEH、∠DFI，得到图②．

（1）在图①中，当α=20°，β=50°时，求∠EPF的度数；

（2）在（1）的条件下，求图②中∠END与∠CFI的度数；

（3）在图②中，当FI∥EH时，请求出α与β的数量关系．

Answer 1

【答案】（1）70°；（2）40°，80°；（3）α+β=90°.

【解析】

(1)由PM∥AB根据两直线平行，内错角相等可得∠EPM=∠AEP=20°，根据平行公理的推论可得PM∥CD，继而可得∠MPF=∠CFP=50°，从而即可求得∠EPF；

(2)由角平分线的定义可得∠AEH=2α=40°，再根据AD∥BC，由两直线平行，内错角相等可得∠END=∠AEH=40°，由对顶角相等以及角平分线定义可得∠IFG=∠DFG=β=50°，再根据平角定义即可求得∠CFI的度数；

(3)由(2)可得，∠CFI=180°-2β，由AB∥CD，可得∠END=2α，当FI∥EH时，∠END=∠CFI，据此即可得α+β=90°．

(1)∵PM∥AB，α=20°，

∴∠EPM=∠AEP=20°，

∵AB∥CD，PM∥AB，

∴PM∥CD，

∴∠MPF=∠CFP=50°，

∴∠EPF=20°+50°=70°；

(2)∵PE平分∠AEH，

∴∠AEH=2α=40°，

∵AD∥BC，

∴∠END=∠AEH=40°，

又∵FG平分∠DFI，

∴∠IFG=∠DFG=β=50°，

∴∠CFI=180°-2β=80°；

(3)由(2)可得，∠CFI=180°-2β，

∵AB∥CD，

∴∠END=∠AEN=2α，

∴当FI∥EH时，∠END=∠CFI，

即2α=180°-2β，

∴α+β=90°．