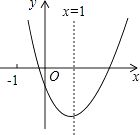题目内容
【题目】已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(﹣1,m)和点B(n,5). 
(1)求该二次函数的关系式;
(2)在给定的平面直角坐标系中,画出这两个函数的大致图象;
(3)结合图象直接写出x2+bx+c>x+1时x的取值范围.
【答案】
(1)解:∵二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(﹣1,m)和点B(n,5),
∴m﹣1+1=0,n=1=5,即n=4,
∴点A(﹣1,0),点B(4,5),
∴ ![]() 解得
解得 ![]() ,
,
∴二次函数的吉祥物为y=x2﹣2x﹣3
(2)解:这两个函数图象如图所示,
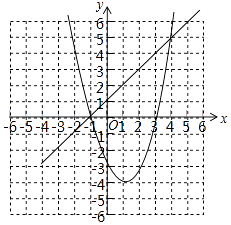
(3)解:由图象可知,x2+bx+c>x+1时,x<﹣1或x>4
【解析】(1)首先求出A、B两点坐标,利用待定系数法即可解决问题.(2)利用描点法画出函数图象即可.(3)根据图象二次函数的图象在一次函数的图象上方,即可写出自变量的取值范围.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目