题目内容
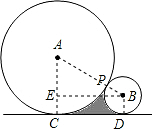
如图,⊙A与⊙B外切于点P,它们的半径分别为6和2,直线CD与它们都相切,切点分别为C,D,则图中阴影部分的面积是( )

A.16
| B.16
| C.16
| D.16
|

连接AC,BD,AB,过点B作BE⊥AC,
所以BE=
=4
,
∵AB=PA+PB=8,
∴sin∠A=
=
,
∴∠A=60°,
∴∠ABE=30°,
∴∠ABD=120°,
梯形ABDC的面积是:
(6+2)•4
=16
;
扇形ACP的面积为
;
扇形BPD的面积为
;
则图中阴影部分的面积=梯形ABDC的面积-扇形ACP的面积-扇形BPD的面积=16
-
π.
故选D.
所以BE=
| 64-16 |
| 3 |
∵AB=PA+PB=8,
∴sin∠A=
| BE |
| AB |
| ||
| 2 |
∴∠A=60°,
∴∠ABE=30°,
∴∠ABD=120°,
梯形ABDC的面积是:
| 1 |
| 2 |
| 3 |
| 3 |
扇形ACP的面积为
| 60π•36 |
| 360 |
扇形BPD的面积为
| 120π•4 |
| 360 |
则图中阴影部分的面积=梯形ABDC的面积-扇形ACP的面积-扇形BPD的面积=16
| 3 |
| 22 |
| 3 |
故选D.


练习册系列答案
相关题目








