��Ŀ����
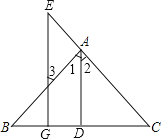
����Ŀ����ͼ��������y1=ax2+bx+c��a��0��ͼ���һ���֣������ߵĶ�������A��1��3������x���һ������B��4��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ�
��2a+b=0��
��abc��0��
�۷���ax2+bx+c=3��������ȵ�ʵ������
����������x�����һ�������ǣ���1��0����
�ݵ�1��x��4ʱ����y2��y1 ��
������ȷ���ǣ� ��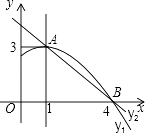
A.�٢ڢ�
B.�٢ۢ�
C.�٢ۢ�
D.�ڢܢ�
���𰸡�C
���������������ߵĶ�������A��1��3����
�������ߵĶԳ���Ϊֱ��x=�� ![]() =1��
=1��
��2a+b=0�����Ԣ���ȷ��
�������߿������£�
��a��0��
��b=��2a��0��
����������y��Ľ�����x���Ϸ���
��c��0��
��abc��0�����Ԣڴ���
�������ߵĶ�������A��1��3����
��x=1ʱ�����κ��������ֵ��
���ax2+bx+c=3��������ȵ�ʵ���������Ԣ���ȷ��
����������x���һ������Ϊ��4��0��
�������ߵĶԳ���Ϊֱ��x=1��
����������x�����һ������Ϊ����2��0�������Ԣܴ���
��������y1=ax2+bx+c��ֱ��y2=mx+n��m��0������A��1��3����B�㣨4��0��
�൱1��x��4ʱ��y2��y1�����Ԣ���ȷ��
���Դ��ǣ�C��
�����㾫����������Ҫ�����˶��κ���ͼ���Լ�ϵ��a��b��c�Ĺ�ϵ����������������Ľ�������֪ʶ�㣬��Ҫ���ն��κ���y=ax2+bx+c�У�a��b��c�ĺ��壺a��ʾ���ڷ���a>0ʱ�������߿�������; a<0ʱ�������߿�������b��Գ����йأ��Գ���Ϊx=-b/2a;c��ʾ��������y��Ľ������꣺��0��c����һԪ���η��̵Ľ������Ӧ�Ķ��κ�����ͼ����x��Ľ������꣮���һԪ���η����е�b2-4ac���ڶ��κ����б�ʾͼ����x���Ƿ��н��㣮��b2-4ac>0ʱ��ͼ����x�����������㣻��b2-4ac=0ʱ��ͼ����x����һ�����㣻��b2-4ac<0ʱ��ͼ����x��û�н��㣮������ȷ�����⣮

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�����Ŀ��ijѧУΪ���˽���꼶Ů����������ѵ�����������ʱ�������ȡ10��Ů�����ԣ��ɼ����±���ʾ����ô��10��Ů�����Գɼ�����������λ�������ǣ� ��
����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�ɼ�/�� | 48 | 49 | 52 | 47 | 51 | 53 | 52 | 49 | 51 | 49 |
A.52��51
B.51��51
C.49��49
D.49��50